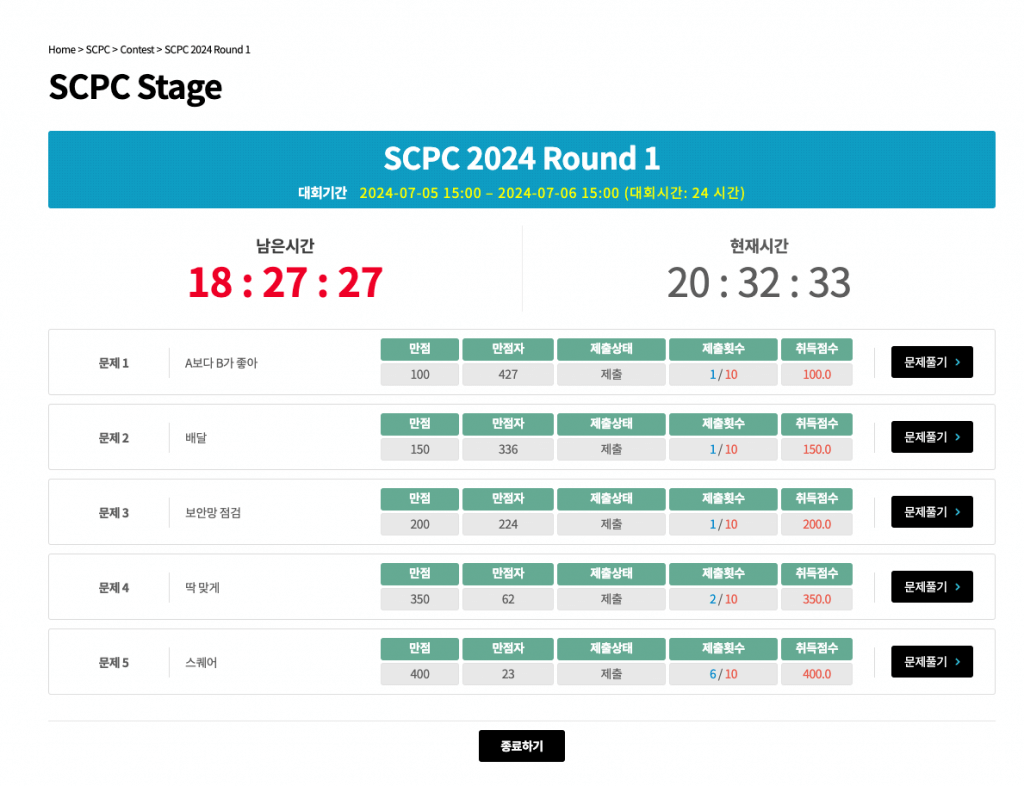
적당히 쉬엄쉬엄 풀어서 난이도에 비해 남은 시간이 다소 적습니다. 올해는 2번까지 풀지 않으면 Round 2를 가기 좀 힘들지 않을까 싶을 정도로 1, 2, 3번이 쉬웠습니다.
개인적인 난이도는 1 < 2 < 3 < 5 < 4번이었습니다.
1차 1번 – A보다 B가 좋아
길이 $N \le 300\,000$의 A와 B로만 이루어진 문자열이 있습니다. 이 문자열에서 길이 $2$ 이상의 어느 부분 문자열을 골라도 A의 개수보다 B의 개수가 크거나 같도록 하고 싶습니다. 원하는 위치에 B를 추가할 수 있다고 할 때 최소 몇 개를 추가해야 할까요?
작은 경우부터 생각해 봅시다.
길이 $2$인 부분 문자열은 AA인 경우만 피하면 됩니다.
길이 $3$인 부분 문자열은 AAA, AAB, ABA, BAA가 있는데, AA라는 부분 문자열을 어떻게 다 없앴다고 가정하면, ABA만 피하면 됩니다.
AA와 ABA를 어떻게 다 없앴다고 가정하면, 길이 $4$인 부분 문자열은 무조건 A의 개수보다 B의 개수가 크거나 같음을 알 수 있습니다.
이 성질이 길이 $5$ 이상에서도 성립하는지 알아봅시다. 귀납법을 사용할 수 있습니다.
- 길이 $K$의 문자열이
A로 끝나는 경우,AA와ABA패턴이 존재하지 않으므로,BBA로 끝나야 합니다. 따라서 이 경우 뒤에서A와B한 글자씩 총 두 글자를 뗀 길이 $K-2$의 문자열에서 성질을 만족했다면, 길이 $K$의 문자열에서도 성질이 유지됩니다. - 길이 $K$의 문자열이
B로 끝나는 경우, 길이 $K-1$의 문자열의 맨 뒤에B를 하나 붙여 준다고 생각할 수 있습니다. 따라서 이 경우 길이 $K-1$의 문자열에서 성질을 만족했다면, 길이 $K$의 문자열에서도 성질이 유지됩니다.
따라서, A와 A 사이에 두 개 이상의 B가 있도록 추가해 주는 것으로 충분합니다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using pii = pair<int, int>;
int main() {
cin.tie(nullptr), ios::sync_with_stdio(false);
int t;
cin >> t;
for (int _ = 1; _ <= t; _++) {
int n;
cin >> n;
string str;
cin >> str;
vector<int> idxs;
for (int i = 0; i < n; i++) {
if (str[i] == 'A') idxs.emplace_back(i);
}
int s = 0;
for (int i = 0; i + 1 < idxs.size(); i++) {
int d = idxs[i + 1] - idxs[i] - 1;
s += max(0, 2 - d);
}
cout << "Case #" << _ << endl;
cout << s << endl;
}
return 0;
}
1차 2번 – 배달
물건이 $N \le 300\,000$개 있습니다. $N$은 $4$의 배수입니다. 물건들에는 무게가 있습니다($1 \le \text{무게} \le 1\,500\,000$).
$4$개의 물건씩 골라 $N$개의 물건을 모두 배송할 예정입니다. 이 때, $4$개의 물건의 무게가 각각 $a \le b \le c \le d$라고 할 때, $$|d-c|+|c-b|+|b-a|+|a-d|$$원을 벌 수 있습니다. 모든 물건을 배달해서 벌 수 있는 최대 금액은 얼마일까요?
$a$, $b$, $c$, $d$의 대소가 이미 정해져 있으므로 절댓값 기호는 의미가 없습니다. 식을 정리합시다.
$$\begin{aligned}& |d-c|+|c-b|+|b-a|+|a-d| \\ =\, & (d-c)+(c-b)+(b-a)+(d-a) \\ =\, & 2d-2a\end{aligned}$$
따라서 가장 무거운 하나와 가장 가벼운 하나만이 배송비에 관여한다는 사실을 알 수 있습니다.
가장 무거운 물건들의 합을 최대화하고, 가장 가벼운 물건들의 합을 최소화하는 방법은 가장 무거운 $N/4$개의 물건들을 $d$로 배정하고, 가장 가벼운 $N/4$개의 물건을 $a$로 배정하도록 하는 것입니다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using pii = pair<int, int>;
int main() {
cin.tie(nullptr), ios::sync_with_stdio(false);
int t;
cin >> t;
for (int _ = 1; _ <= t; _++) {
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
sort(a.begin(), a.end());
int m = n / 4;
ll s = 0;
for (int i = 0; i < m; i++) s -= a[i];
for (int i = 3 * m; i < n; i++) s += a[i];
cout << "Case #" << _ << endl;
cout << s * 2 << endl;
}
return 0;
}
1차 3번 – 보안망 점검
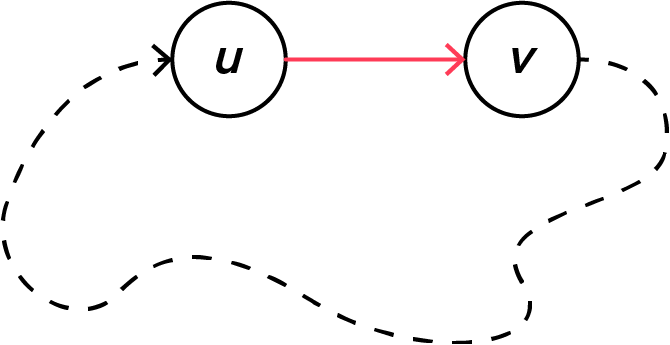
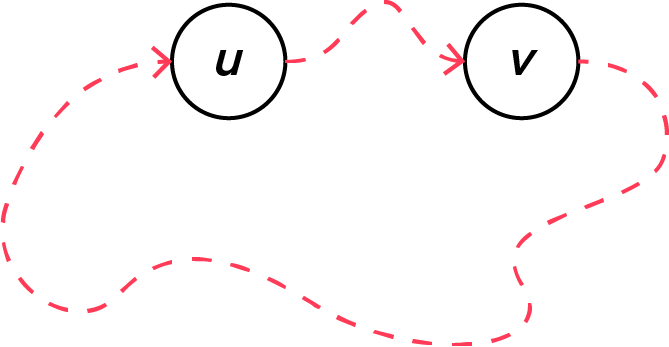
보안 장비 $N \le 300\,000$개가 있습니다. 이들은 총 $N+1$개의 라인으로 연결되어 있으며, 이 중 $N$개의 라인은 보안 장비 $N$개를 원형으로 연결하고 있으며, 나머지 $1$개의 라인은 원형으로 연결되어 있는 보안 장비들 중 두 개를 잇습니다. 이 때, 정확히 $2$개의 라인이 파괴되었을 때 망이 분리되는 경우의 수를 구해야 합니다.
다시 말하면, 보안 장비 그래프는 $3$개의 사이클로 되어 있으며, 가장 큰 사이클은 크기가 $N$입니다.
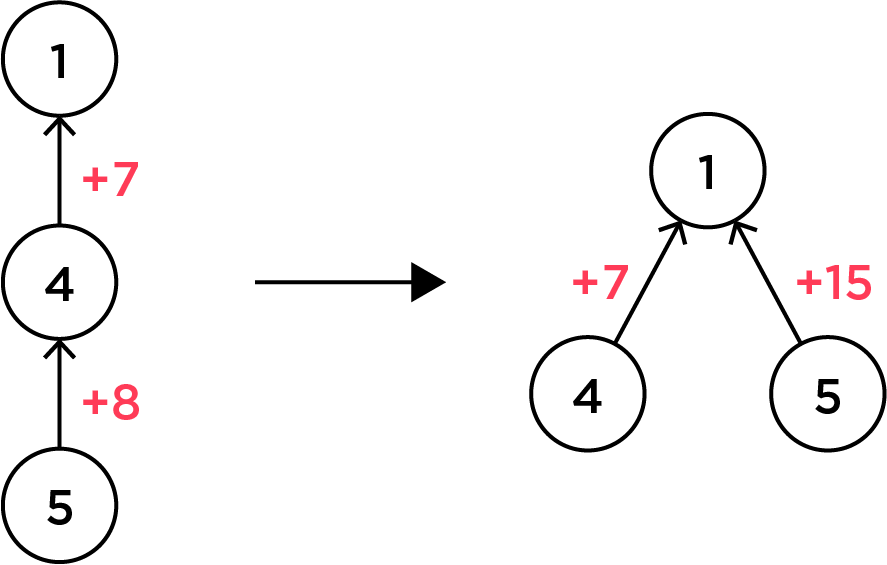
큰 사이클을 나누는 한 개의 간선은 degree가 $3$인 정점 두 개를 찾는 것으로 찾을 수 있습니다. 그 한 개의 간선을 기준으로 왼쪽과 오른쪽에 간선이 몇 개 있나 확인합니다. 각각 $l$개와 $r$개가 있다면, 그래프를 분할하는 경우의 수는 $$\frac{l\left(l-1\right)}{2}+\frac{r\left(r-1\right)}{2}$$개임을 확인할 수 있습니다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using pii = pair<int, int>;
ll solve() {
int n;
cin >> n;
vector<vector<int>> graph(n + 1);
vector<int> deg(n + 1, 0);
for (int i = 0; i <= n; i++) {
int u, v;
cin >> u >> v;
graph[u].emplace_back(v);
graph[v].emplace_back(u);
deg[u]++, deg[v]++;
}
vector<int> deg3;
for (int u = 1; u <= n; u++) {
if (deg[u] == 3) {
deg3.emplace_back(u);
}
}
assert(deg3.size() == 2);
int a = deg3[0], b = deg3[1];
ll l1 = 0, l2 = 0;
function<int(int, int)> dfs = [&](int u, int p) {
if (u == b) return 0;
for (int v: graph[u]) {
if (v == p) continue;
return dfs(v, u) + 1;
}
};
bool skip_flag = false;
for (int c: graph[a]) {
if (c == b && !skip_flag) {
skip_flag = true;
continue;
}
if (l1) {
l2 = 1 + dfs(c, a);
} else {
l1 = 1 + dfs(c, a);
}
}
ll s = 0;
s += (l1) * (l1 - 1) / 2;
s += (l2) * (l2 - 1) / 2;
return s;
}
int main() {
cin.tie(nullptr), ios::sync_with_stdio(false);
int t;
cin >> t;
for (int _ = 1; _ <= t; _++) {
cout << "Case #" << _ << endl;
cout << solve() << endl;
}
return 0;
}
1차 4번 – 딱 맞게
원소의 개수가 $5 \le N \le 100\,000$개인 두 중복 집합 $A$와 $B$가 있습니다.
여기에 일대일 대응 $F\left(A, B\right)$을 정의하여, 서로 대응하는 원소의 값의 차이의 절댓값들 중 가장 큰 값 $\max F\left(A, B\right)$를 계산할 수 있습니다. 이 값이 $1 \le L \le 10^9$보다 작으면서 가장 크게 되도록 해야 합니다. 이때 $\max F\left(A, B\right)$를 출력해야 합니다.
문제를 쉽게 써 봅시다. 배열 $A$와 $B$가 있어서, 이들의 순서를 잘 섞어서 $$\max \left\{ |a_1-b_1|,|a_2-b_2|,\cdots,|a_N-b_N| \right\}$$을 $L$ 이하가 되게 하면서 최대화하라는 문제입니다.
$A$와 $B$를 각각 정렬하면 $\max F\left(A, B\right)$가 최소가 됩니다. 이 사실을 통해, $A$에서 적당한 한 개의 값 $a$와 $B$에서 적당한 한 개의 값 $b$를 골라 놓고, 나머지 원소들을 정렬해 놓는 방법을 사용할 수 있습니다. 이미 정렬된 $A$와 $B$에 대해서 $|A_i-B_i|$, $|A_{i+1}-B_i|$, $|A_i-B_{i+1}|$의 값들을 미리 계산하여 관리하고 있다면 적당한 $(a,b)$ 쌍에 대해 충분히 빠르게 계산할 수 있습니다.
$|a-b| \le L$인 모든 쌍을 보는 것만으로 문제를 해결하는 데에는 충분합니다. 더 나아가서, $a$가 정해져 있을 때, $|a-b|$의 값이 $L$ 이하이면서 가장 크도록 하는 $b$를 적당히 잘 골라 주고, 이런 $(a,b)$ 쌍들만을 보는 것만으로 충분함을 보일 수 있습니다.
아래 코드의 복잡도는 $\mathcal{O}\left(N \log N\right)$입니다. 제 소스 코드는 세그먼트 트리와 이분 탐색을 쓰지만 단조성을 이용한 투 포인터 등의 방법으로 시간을 더 줄일 수 있습니다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using pii = pair<int, int>;
ll a[100010], b[100010];
ll p[400010], pa[400010], pb[400010];
void update(ll *tree, int x, int s, int e, int i, ll v) {
if (s == e) {
tree[x] = v;
return;
}
int m = (s + e) / 2;
if (i <= m) update(tree, x * 2, s, m, i, v);
else update(tree, x * 2 + 1, m + 1, e, i, v);
tree[x] = max(tree[x * 2], tree[x * 2 + 1]);
}
ll query(ll *tree, int x, int s, int e, int l, int r) {
if (r < s || e < l) return 0;
if (l <= s && e <= r) return tree[x];
int m = (s + e) / 2;
return max(query(tree, x * 2, s, m, l, r), query(tree, x * 2 + 1, m + 1, e, l, r));
}
void update_p(int i, ll v) {
update(p, 1, 1, 100000, i, v);
}
void update_pa(int i, ll v) {
update(pa, 1, 1, 100000, i, v);
}
void update_pb(int i, ll v) {
update(pb, 1, 1, 100000, i, v);
}
ll query_p(int l, int r) {
if (l > r) return 0;
return query(p, 1, 1, 100000, l, r);
}
ll query_pa(int l, int r) {
if (l > r) return 0;
return query(pa, 1, 1, 100000, l, r);
}
ll query_pb(int l, int r) {
if (l > r) return 0;
return query(pb, 1, 1, 100000, l, r);
}
ll solve() {
ll n, l;
cin >> n >> l;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) cin >> b[i];
sort(a + 1, a + 1 + n);
sort(b + 1, b + 1 + n);
for (int i = 1; i <= n; i++) update_p(i, abs(a[i] - b[i]));
for (int i = 1; i + 1 <= n; i++) update_pa(i, abs(a[i + 1] - b[i]));
for (int i = 1; i + 1 <= n; i++) update_pb(i, abs(a[i] - b[i + 1]));
ll ans = -1;
for (int ai = 1; ai <= n; ai++) {
for (ll x: {a[ai] - l, a[ai] + l}) {
int biv = lower_bound(b + 1, b + 1 + n, x) - b;
for (int bi: {biv - 1, biv}) {
if (bi < 1 || bi > n) continue;
// move ai and bi to the end; calculate max abs diff of the rest
ll mx = abs(a[ai] - b[bi]);
mx = max(mx, query_p(0, min(ai, bi) - 1));
if (ai > bi) {
mx = max(mx, query_pb(bi, ai - 1));
} else {
mx = max(mx, query_pa(ai, bi - 1));
}
mx = max(mx, query_p(max(ai, bi) + 1, n));
if (mx <= l) ans = max(ans, mx);
}
}
}
return ans;
}
int main() {
cin.tie(nullptr), ios::sync_with_stdio(false);
int t;
cin >> t;
for (int _ = 1; _ <= t; _++) {
cout << "Case #" << _ << endl;
cout << solve() << endl;
}
return 0;
}
1차 5번 – 스퀘어
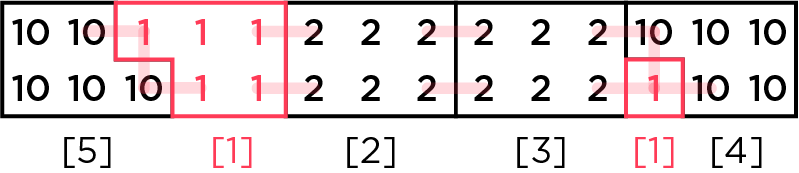
배열에서 $2$ 이상의 정수 $k$를 정해서, $k$개의 $k$를 $1$개의 $k^2$로 바꾸는 작업을 ‘스퀘어’라고 정의합시다. 예를 들어, $$\begin{aligned}& [\textcolor{#ff3b57}{2},4,\textcolor{#ff3b57}{2},4,2,2] \\ \rightarrow\, & [4,4,4,\textcolor{#ff3b57}{2},\textcolor{#ff3b57}{2}] \\ \rightarrow\, & [\textcolor{#ff3b57}{4},\textcolor{#ff3b57}{4},\textcolor{#ff3b57}{4},\textcolor{#ff3b57}{4}] \\ \rightarrow\, & [16] \end{aligned}$$과 같이 스퀘어 연산을 수행할 수 있습니다.
크기 $N \le 50\,000$의 배열이 있습니다. 각 원소는 $1$ 이상 $10^9$ 이하입니다. $Q \le 50\,000$개의 쿼리를 처리해야 합니다.
- $l$ $r$: 배열 $a_l$, $a_{l+1}$, $\cdots$, $a_r$에서 가능한 ‘스퀘어’의 최대 횟수를 구하여 출력한다.
배열에서 $2$ 미만 및 $50\,000$ 초과인 원소들은 무시해도 된다는 사실과, ‘스퀘어’ 연산의 연쇄 반응은 최대 $4$번까지만 일어난다는 사실을 생각해 봅시다. 세그먼트 트리로는 어떻게 풀어야 될지 감이 잘 안 잡히지만, Mo’s는 사용하기 좋아 보입니다. 아래 코드의 시간 복잡도는 $\mathcal{O}\left(N + Q \log Q + Q \sqrt{N} \log \log N \right)$입니다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using pii = pair<int, int>;
const int m = 240;
int a[50001], cnt[50001];
ll ans[50000];
struct query {
int l, r, i;
query() : l(0), r(0), i(0) {}
query(int l, int r, int i) : l(l), r(r), i(i) {}
bool operator<(const query &rhs) const {
return pii(l / m, r) < pii(rhs.l / m, rhs.r);
}
};
void init(ll &val) {
for (int x = 2; x <= 50000; x++) {
int t = x * x;
if (2 <= t && t <= 50000) {
cnt[t] += cnt[x] / x;
}
val += cnt[x] / x;
}
}
void add(ll &val, int x) {
while (2 <= x && x <= 50000) {
cnt[x]++;
if (cnt[x] % x) return;
val++;
x *= x;
}
}
void remove(ll &val, int x) {
while (2 <= x && x <= 50000) {
cnt[x]--;
if ((cnt[x] + 1) % x) return;
val--;
x *= x;
}
}
// sqrt 50 000 < 224
// sqrt sqrt 50 000 < 15
// sqrt sqrt sqrt 50 000 < 4
// sqrt sqrt sqrt sqrt 50 000 < 2
void solve() {
int n;
cin >> n;
memset(cnt, 0, sizeof cnt);
for (int i = 1; i <= n; i++) cin >> a[i];
int q;
cin >> q;
vector<query> qry(q);
for (int i = 0; i < q; i++) {
int l, r;
cin >> l >> r;
qry[i] = query(l, r, i);
}
sort(qry.begin(), qry.end());
ll val = 0;
int l = qry[0].l, r = qry[0].r;
for (int i = l; i <= r; i++) {
if (2 <= a[i] && a[i] <= 50000) cnt[a[i]]++;
}
init(val);
ans[qry[0].i] = val;
for (int i = 1; i < q; i++) {
while (l < qry[i].l) remove(val, a[l++]);
while (l > qry[i].l) add(val, a[--l]);
while (r > qry[i].r) remove(val, a[r--]);
while (r < qry[i].r) add(val, a[++r]);
ans[qry[i].i] = val;
}
for (int i = 0; i < q; i++) cout << ans[i] << '\n';
}
int main() {
cin.tie(nullptr), ios::sync_with_stdio(false);
int t;
cin >> t;
for (int _ = 1; _ <= t; _++) {
cout << "Case #" << _ << '\n';
solve();
}
return 0;
}