[latexpage]
‘기억하기 쉽고 안전한’ 비밀번호?
인터넷을 사용하다 보면 어느 서비스든 회원가입을 할 때가 생깁니다. 그리고, 회원가입을 하려면 대부분 비밀번호를 새로 만들어야 합니다. 예전에는 쉽게 만들었던 것 같은데, 대문자 소문자 숫자 특수문자를 다 써서 만들라니 기가 찹니다.
비밀번호 생성기를 켜 봅시다. 인터넷뱅킹에 쓰려고 10자리의 비밀번호를 만들었더니 bet8qU_r#u라는 한 눈에 봐도 강력해 보이는 비밀번호가 나왔습니다. 근데 별로 기억하기는 쉽지 않아 보입니다. 그래도 은행 비밀번호인데 어디다 적어 두자니 남이 볼까 두렵고, 외우자니 시간이 꽤 걸릴 것 같습니다.
‘기억하기 쉬운 비밀번호’와 ‘안전한 비밀번호’는 모순적인 존재들인 것 같습니다. 그런데, 정말 그럴까요?
안전한 비밀번호
- 이미 비밀번호가 충분히 안전하신 분들께서는 이 부분을 스킵하고 ‘기억하기 쉬운 비밀번호‘부터 보셔도 됩니다!
애초에 ‘안전한 비밀번호’를 왜 만드는 걸까요? 보통은 원하지 않는 사람이 멋대로 내 계정으로 로그인하지 못하게 하기 위함입니다. ‘원하지 않는 사람’이라 함은 비밀번호를 멋대로 알아낼 수 있는 – 일반적으로는 – 해커들이죠.
일단 우리가 가입한 사이트는 비밀번호를 암호화해서 저장한다고 가정합시다. (사실 모든 사이트가 그래야 하지만요. 2017년에 평문으로 비밀번호 저장하는 사이트를 구축하는 웹 개발자는 당장 해고해야 마땅합니다.)
그럼 해커는 어떤 방식으로 비밀번호를 알 수 있을까요? 만약 우리의 암호화된 비밀번호를 입수했다고 해도, 무차별 대입 공격(bruteforcing) 외에는 방법이 없습니다.
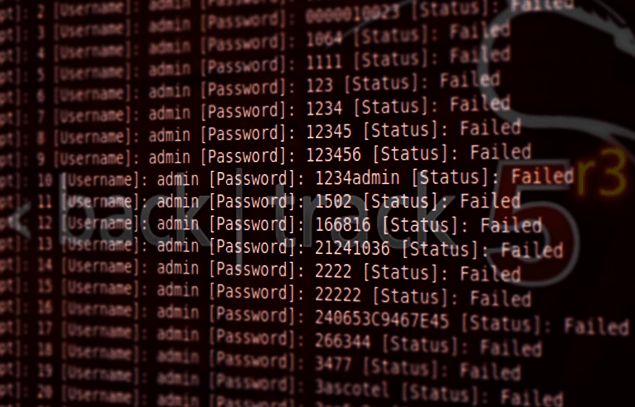
암호화는 이런 방식으로 동작합니다. 만약 제가 이 사이트의 관리자 비밀번호를 shift.moe123으로 설정했다고 합시다. 그러면 서버는 (SHA-256 알고리즘을 쓴다면) 비밀번호를 그대로 저장하는 게 아니라, 이런 식으로 저장합니다:
98086156AA56FE8A7D5AC35D4EA21A49A776505B869CC76829CCD93BAC91A3F9
이것을 해시라고 합니다. 해시는 비밀번호마다 다릅니다. 그래서 서버가 맞는 비밀번호인지 체크하려면 사용자가 입력한 비밀번호를 해시로 만들어서 그 값이 똑같은지 체크합니다. 예를 들어 shift.moe123의 해시 값은 항상 위의 해시 값과 같습니다.
그리고 비밀번호가 조금만 바뀌어도 해시 값은 몰라보게 변합니다. 가령 딱 한 글자만 바꾼 shift.moe124의 SHA-256 해시는
66CFE1B558388800107E5E0CE4AADE6866F8FCE147D7D41108D7E930AD923DD5
입니다. 위의 해시와 아래 해시는 전혀 연관이 없어 보입니다.
해시를 통해 원래 비밀번호를 알 수 있는 방법은 … 두 가지가 있습니다. 무작위로 대입해 보는 방법과 암호화 알고리즘을 분석해 알아내는 방법이 있는데요, 후자는 현재로서는 몇십 년동안 천문학적인 액수를 투자해 해시 하나를 풀 수 있습니다. 해커들은 당연히 그럴 만한 가치를 느끼지 못하고 무작위 대입을 시작하는 것입니다.
무작위 대입 전략
해커가 만약 사이트의 모든 유저에 대한 정보 – 비밀번호 해시 값을 포함해서 – 를 담고 있는 데이터베이스를 입수했다고 합시다. 이 때 타겟은 누구일까요? 보통은 어떻게든 해시 값을 생성해서 얻어걸리는 사람의 계정을 탈취해 갈 것입니다. 어떤 계정이든, 로그인만 할 수 있다면 그걸로 카페에 들어가서 게시글을 도배하든 금융거래를 하든 나름대로의 의미가 있을 테니까요.
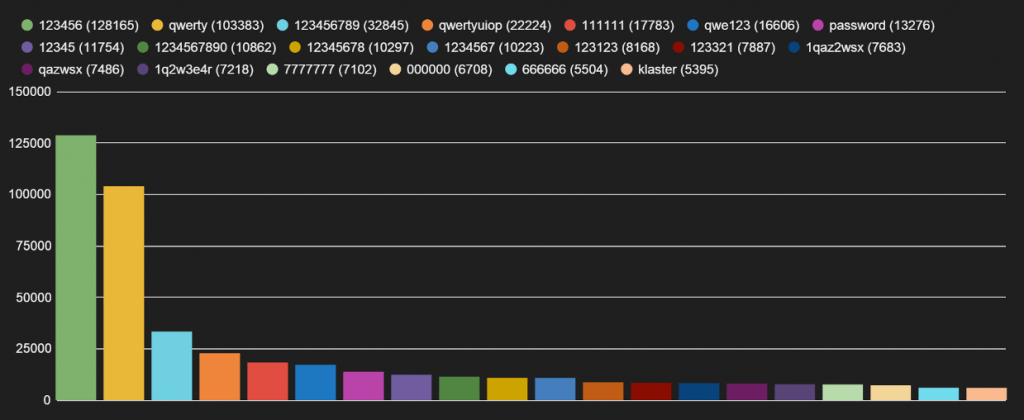
일단 해커는 먼저 사람들이 가장 자주 사용하는 비밀번호들부터 대입해 볼 것입니다. 1234, 123456, qwerty 같은 비밀번호들이 대표적인 예입니다. 가장 먼저 얻어걸리는 비밀번호들이죠. 위 사이트에 의하면, 아직도 저 리스트에 있는 상위 1,000개의 비밀번호를 전체 91%의 사용자들이 사용하고 있다고 합니다. 보통 SHA-256 키 하나를 대입하는 건 초당 260만번 할 수 있으니 위의 리스트에 있는 비밀번호를 사용 중이라면 고작 0.001초도 안 되어 전부 드러나버릴 수 있습니다.
그런데 요즘은 사이트에서 회원가입을 할 때부터 이런 비밀번호를 못 쓰게 막고 있습니다. 그런 사이트에서는 저런 비밀번호를 사용하는 사람이 애초에 없다는 것일 테고, 해커가 얻어갈 수 있는 이득도 없다는 거나 마찬가지입니다.
그런 해커들이 다음으로 시도해 보는 게 무작위 단어 대입입니다. 사전에 있는 단어들을 조합해서, 처음부터 끝까지 대입해 보는 것이죠. 만약 사전에 있는 단어만으로 만들어진 비밀번호라면 사전에 적혀 있는 단어 수에 따라 다르겠지만, 영어 단어 30만개를 대입한다면 단어 한 개짜리 비밀번호는 대략 0.115초만에, 단어 두 개짜리 비밀번호는 길게는 9시간 35분까지 걸리겠네요. 다시 말하지만 해커는 수많은 정보 중 얻어걸리기만 하면 되기 때문에 9시간 35분은 투자할 가치가 있는, 굉장히 짧은 시간입니다.
무작위 단어 대입을 해도 별 수확을 못 얻었다면 모든 문자를 무작위로 대입하기 시작합니다. 그런데 이건 단점이 조금 있습니다. 비밀번호가 한 자리수 늘어날 때마다 시도해야 되는 가짓수도 배로 늘어난다는 겁니다.

만약 숫자로만 된 비밀번호를 먼저 때려맞추자고 합시다. 숫자는 총 10개가 있으니까 한 자리에 올 수 있는 글자가 10개입니다. 그러니까, 한 자리수 비밀번호를 맞추려면 10번 시도하면 됩니다. 두 자리수는 $10 \times 10 = 100$번 시도하면 되겠군요, $n$자리수의 비밀번호에 대해서는 $10^n$번 시도하면 풀리겠죠?
초당 260만번 대입할 수 있다고 했으니, 4자리 비밀번호는 $\dfrac{10^4}{2,600,000} \approx 0.000385$초, 8자리 비밀번호는 $\dfrac{10^8}{2,600,000} \approx 38.466$초가 걸리겠군요. 한 자리가 늘어날 때마다 걸리는 시간은 10배씩 늘어날 겁니다. 그럼 여기에 알파벳 소문자를 섞으면 어떨까요?
알파벳 소문자는 총 26문자가 있으니까 이걸 숫자와 섞으면 한 자리에 총 36개의 문자가 올 수 있고, $n$자리수의 비밀번호에 대해서는 $36^n$번 시도하면 풀리겠습니다. 4자리 비밀번호는 $\dfrac{36^4}{2,600,000} \approx 0.6460$초, 8자리 비밀번호는 $\dfrac{36^8}{2,600,000} \approx 1,085,042.3$초, 즉 12일 13시간 24분 가량이 걸립니다. 같은 8자리인데, 숫자만 썼을 때는 1분도 안 되던 게 소문자만 섞었는데도 2주가 가까히 걸리게 되었습니다.
그럼, 걸리는 시간을 표로 정리해 보겠습니다.
| 글자 수 | 4글자 | 8글자 | 10글자 | 12글자 | |
| 숫자 | 10 | 0초 | 38초 | 1시간 4분 | 4.45일 |
| 소문자 | 26 | 0초 | 22시간 18분 | 1.72년 | 1,163년 |
| 숫자 + 소문자 |
36 | 1초 | 12.56일 | 44.59년 | 5.78만 년 |
| 숫자 + 소문자 + 특수문자(8) |
44 | 1초 | 62.54일 | 331.7년 | 64.2만 년 |
| 숫자 + 소문자 + 대문자 |
62 | 6초 | 2.66년 | 1.02만 년 | 3935만 년 |
| 숫자 + 소문자 + 대문자 + 특수문자(8) |
70 | 9초 | 7.03년 | 3.45만 년 | 1.69억 년 |
이런 이유로 많은 사이트들은 숫자, 소문자, 대문자, 특수문자를 섞어서 비밀번호를 만들 것을 권장하고 있습니다.
문제가 있다면, 숫자, 소문자, 대문자, 특수문자를 전부 섞어서 비밀번호를 정말 복잡하게 만들었는데, 이걸 기억하기가 어렵다는 것입니다.
기억하기 쉬운 비밀번호
그러면 ‘기억하기 쉬운’ 건 무엇일까요?
사람마다 기억하기 어렵고 쉬운 것은 다르겠지만, 일반적으로는 비밀번호에 어떤 의미를 부여하면 기억하기 쉬워지는 것 같습니다. 아무 의미도 없는 이상한 문자열 말고, 예를 들어.. 제가 지금 배고프니까 음식 이름으로 비밀번호를 만들어 봅시다. 비밀번호를 뚫는 데 얼마나 걸릴지는 여기에서 테스트해 볼 수 있습니다.

최근 가격인상으로 말 많은 BBQ 치킨입니다. #Golden_Olive_Chicken이라는 비밀번호를 생각해낼 수 있겠습니다. 위 사이트에 넣어 본 결과 이 비밀번호를 뚫는 데는 1해 7,600경($=1.76\times10^{20}$)년이 필요하다고 합니다. 숫자는 없지만 대소문자와 특수문자가 적절하게 섞였고, 기억하기 쉬우면서 무려 21글자나 됩니다. 배고플 때는 로그인하기 조금 그렇겠지만, 충분히 강력한 비밀번호 같네요!
혹은 노래 가사에서도 비밀번호를 생각해낼 수 있을 것 같습니다.

벌써 발표된 지 4년이 넘어간 곡입니다. 시간 참 빨리 가는 것 같습니다.. I'm_a_mother_father_gentleman_130412 정도를 생각할 수 있을 것 같습니다. 가사만으로는 예측하기 쉬울 수도 있으니 뒤에 발매일을 붙여줬습니다. 특수문자, 대소문자, 숫자 모두가 포함된 36글자의 강력하고 기억하기 쉬운 비밀번호입니다. $1.82\times10^{53}$년이 걸려야 뚫을 수 있습니다.
혹은, 한글 문장을 키보드로 그냥 쳐서 비밀번호를 만들 수 있습니다. 예를 들어.. ‘웃으면서 미래의 이야기를 합시다’는 dntdmaustj_alfodml_dldirlfmf_gkqtlek 정도가 되겠네요, 소문자와 특수문자밖에 없지만 충분히 길기 때문에 $9.0\times10^{39}$년이 걸립니다.
쌍자음이 있으면 대문자를 만들 수 있으니까(영어 키보드는 Shift를 누르면서 글자를 누르면 대문자가 됩니다) ‘대한민국의 주권은 국민에게 있다’는 eogksalsrnrdml_wnrnjsdms_rnralsdprp_dlTek가 됩니다. 무려 41글자, $5.86\times10^{56}$년이 걸리는군요!
이런 식으로 기억하기 쉽고 강력한 비밀번호를 만들 수 있습니다. 취약하거나 기억하기 어려운 비밀번호들은 지금 다시 만들어보는 게 어떨까요?