2024년 회고
올해는 블로그에 글을 많이 쓰지 못했습니다. 아쉬운 일입니다. 그만큼 바쁘게 살았다는 뜻도 될 것 같습니다. 여전히 저는 GPT를 사용하지 않고 수제 포스트를 작성하고 있으므로 많은 양해를 부탁드립니다…
여러 게임들에서 모닥불은 흥미로운 장치입니다. 모닥불 밖은 수많은 난관과 적들로 바글바글하지만, 모닥불에서만큼은 안심하고 쉬어갈 수 있고, 앞으로 어떻게 하면 좋을지 고민하면서 재정비할 수 있는, 하지만 언젠가 떠나야 한다는 것을 알고 있는, 그런 곳입니다.
이제 먹고 사는 문제를 생각해야 될 때가 되었습니다. 그 전에 고민하는 시간을 가져 보려고 합니다.
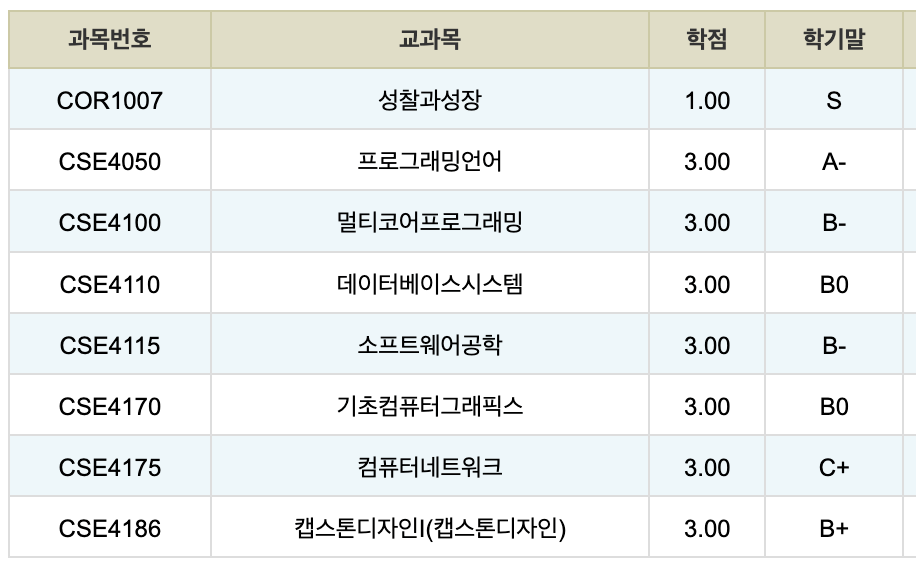
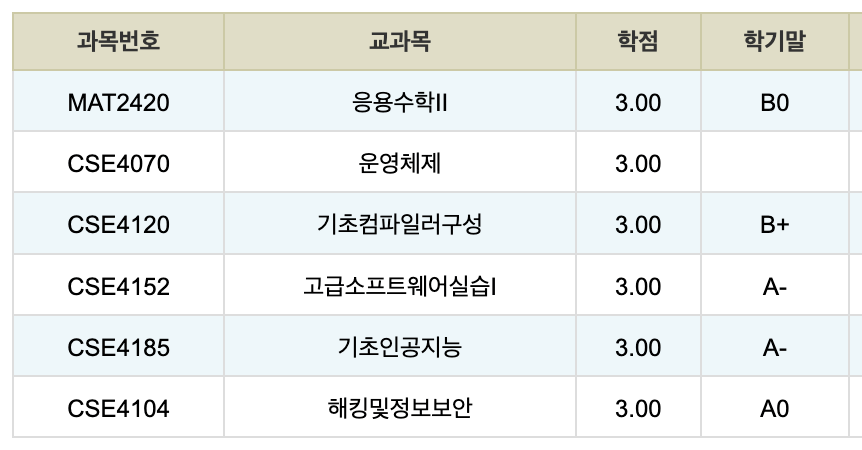
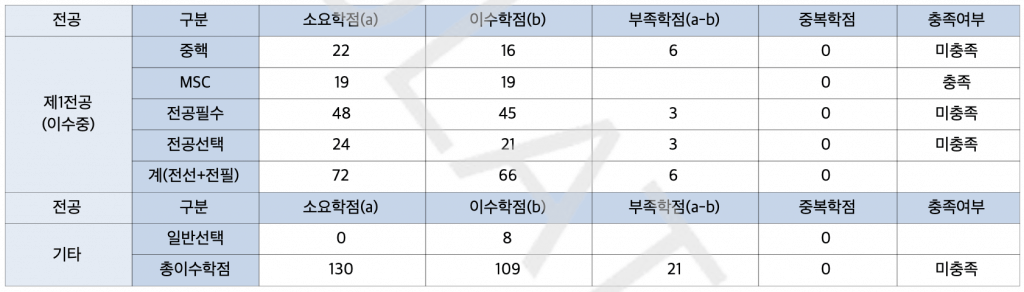
졸업


결국 졸업을 하네요. 사실 큰 감흥은 없는 것 같습니다. 대학 생활은 참 길었습니다. 2018년에 입학했으니 7년을 다녔던 셈이 됩니다. 학교에 들어오기 위해서 수험생활을 했던 글을 돌아보는데, 그때의 나와 지금의 나는 참 다른 생각을 하고 있구나 같은 생각이 들었습니다.
지금 와서 말하는 거긴 하지만, 사실 18수능 당시에 앞자리 수험생의 수학 30번 답안을 봤습니다. 보려고 해서 본 건 아니고, 문제를 풀다 앞을 봤는데 OMR에 마킹되어 있는 수가 또렷이 보였습니다.
’21’.
하지만 그걸 보고도 제가 마킹한 답은 ’42’였습니다. 그 수험생이 설마 정답을 냈을 거라고 생각하지 않았던 것도 있고, ‘베낀다’는 행위부터가 마음을 불편하게 하기에 충분했기 때문입니다. 만약 눈 딱 감고 베꼈으면 학교가 달라졌겠다 싶습니다 . 흔히들 서강대생들 은 소위 ‘연고대’에 떨어져서 오기 때문에 특유의 내재된 자격지심이 있다고들 하는데, 입학 당시에 ‘그때 30번을 베꼈으면!’이라던가, ”간판’을 낮추고 다른 학교를 갈 걸!’ 같은 생각을 안 했다면 거짓말일 테니, 그렇게 틀린 말은 아닌 것 같습니다.
지금은 전혀 그렇게 생각하지 않습니다. 2018년의 ACM-ICPC Team이 없었으면 제가 문제해결을 이렇게까지 좋아하는 사람이 됐을 리가 없습니다. 그리고 그러다가 맡게 된 학회장이라는 역할은, 극히 내향적이고 남들 앞에 잘 나서지 못하던 제 성격을 180° 바꿔놓았습니다(그렇다고 아직 ‘외향적’이라고 할 수는 없을 것 같네요). 가장 중요하게는, 제가 서강대를 가지 않았다면 솔브드도 없었을 거라는 건 틀림없습니다. 물론 자료구조 성적을 별 시덥잖은 이유로 B+ 주는 등 마음에 안 드는 점들도 있기야 하지만 이곳에서의 학교생활은 지금의 저를 만든 중요한 조각이 되었습니다.
더구나 집안 형편이 어려운 와중에 4년간 학비를 전액 지원받아 다니면서 정말로 하고 싶은 일들에 열정을 쏟을 수 있었던 점은 정말로 학교에 감사한 점입니다. 다만 학교가 제게 해 준 것에 비해 제가 그렇게 학교를 열심히 다녔느냐 하면… 처음에는 공부를 좀 열심히 했던 것 같은데 나이를 먹을수록 그렇지 않게 된 것 같고, 수업 안 듣고 문제 풀거나 개발을 했습니다. 죄송합니다. 얼마나 학교의 위상을 올렸을지는 모르겠지만 대회 나가서 상 많이 타 왔으니 용서해주세요…
조교
올해는 CSE4152 문제해결프로그래밍 과목의 학부조교를 했습니다.
위에다 학교 찬양을 마구 해 뒀지만 사실 학교 들어와서는 커리큘럼에 사소한 불만들이 좀 있었습니다. 커리큘럼이 컴퓨터과학을 제대로 배우는 데는 문제가 없긴 했는데요, 몇몇 과목에 아쉬운 부분이 있었습니다. 예를 들어 컴퓨터공학설계및실험I에서는 PHP 프로그래밍과 MFC 어플리케이션 개발을 실습했는데, 회사를 다녀오니 많은 과목들이 최신화되어 있어서 놀랐습니다. 그리고 그 놀람 중 하나는 알고리즘 문제해결 과목의 신설이었습니다.
이주호 교수님의 의지로 신설된 PS 과목은 과제와 시험이 전부 문제해결입니다. 학생들이 엘리스에 코드를 제출하면 실시간 자동 채점을 받습니다. 저는 이번에 과제 데이터를 준비하고 시험 문제를 출제하는 조교 역할을 맡았습니다. 기술적으로는 엘리스 플랫폼 상에서 BOJ의 ‘스페셜 저지’와 ‘인터랙티브’에 해당하는 것들을 구현해야 했던 점이 제일 어려웠지만 제가 나름 재사용 가능하도록 만들어 놨으니 졸업하더라도 이후 조교분께서 아마 활용해서 문제를 만드실 수 있지 않을까 싶습니다. 별개로 엘리스는 문제 수정 시 모든 데이터를 다운받아서 브라우저 메모리에 저장하도록 되어 있어서 큰 데이터를 준비하기 부담스럽고, ‘부분문제’를 만들더라도 한 태스크에서 메모리 초과 시 전체가 0점이 되는 등의 불편함이 있습니다. 부디 외고쳐졌으면 좋겠습니다.
이외에는 문제해결 과목이 생겼다는 데에 큰 의미가 있다고 생각하고, 앞으로도 학생들이 알고리즘 문제해결에 재미를 붙일 수 있는 좋은 계기로 지속적으로 작용할 수 있으면 좋겠습니다. KAIST 등 다른 학교에 문제해결 수업이 있는 게 부러웠는데 이제 남부럽지 않은 학교가 되었네요.
중간고사/기말고사 문제들이 궁금하시다면 BOJ에서 풀어보실 수 있습니다.
솔브드
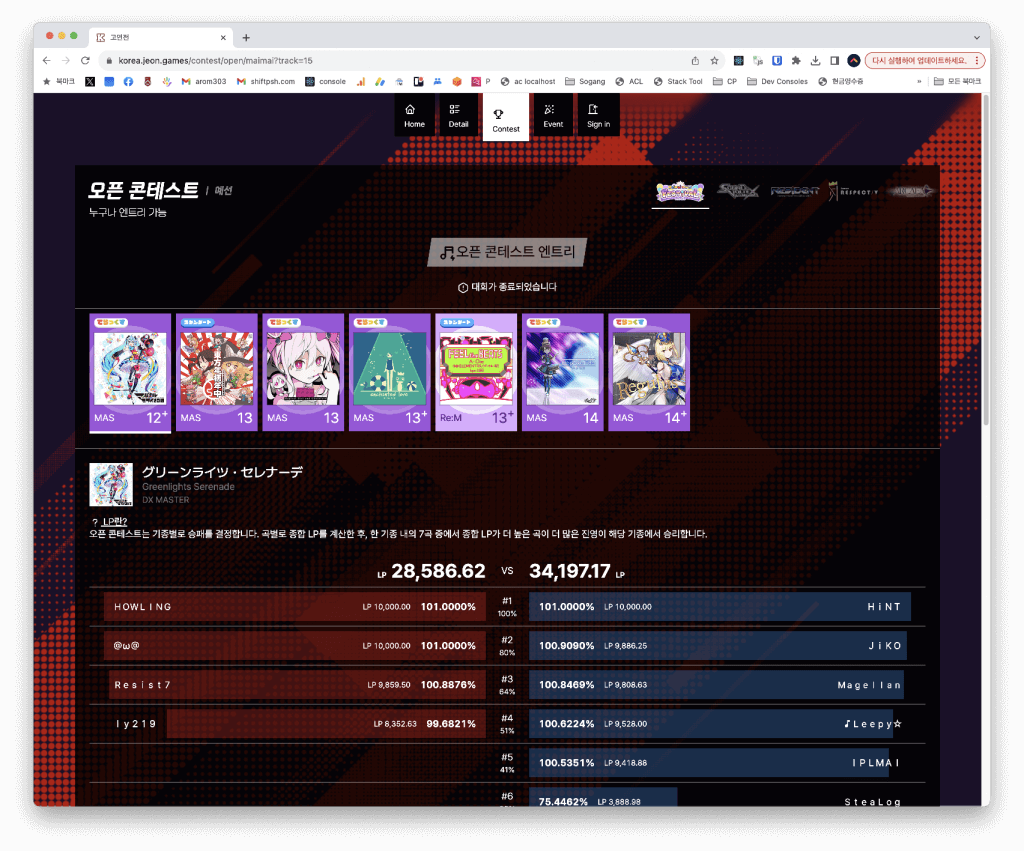
올해 초에 온사이트 프로그래밍 대회인 그랜드 아레나 파티를 개최할 수 있었습니다!

하지만 안타깝게도 이후에 아레나가 더 열리지는 않고 있습니다. 아레나는 레이팅을 매기는 대회이기 때문에 솔브드에서 모든 아레나를 검수해 왔는데, 검수를 수없이 해온 저로서도 아레나 일정에 맞춘 대회 검수는 제 생각보다 훨씬 많은 리소스를 필요로 했고, 급기야 몇몇 대회에서 실제로 문제가 발생하기도 했습니다. 그렇다고 검수를 다른 분께 맡기자면 검수비를 들여야 하는데, 아무리 봐도 수고에 비해 합당한 검수비를 드릴 수 없을 것 같아서, 이걸 해결할 방법을 찾지 못하는 한 당분간 열리지 않을 것 같습니다. 너무 아쉽습니다.

그런가 하면, 솔브드를 전세계 경쟁 프로그래밍 커뮤니티에 소개하는 영광스러운 일도 있었습니다. ICPC 아스타나 월드 파이널 일정 중 하나로 경쟁 프로그래밍 관련 여러 도구 및 방법론을 소개하는 CLI 심포지움이 있는데, 대회 측에서 솔브드를 소개해줬으면 좋겠다고 발표자로 초청해 주셔서 카자흐스탄에 다녀왔습니다. 발표는 영어로 30분간 진행했습니다.
하필이면 제가 마지막 순서고 제 앞에는 코드포스의 KAN님과 앳코더의 maroonrk님이 발표하셔서 정말로 많은 긴장을 했습니다. 청중께서는 주로 ICPC 리저널 콘테스트 디렉터(RCD) 혹은 월드 파이널 스탭이었는데, 다행히도 걱정했던 것과는 달리 반응이 꽤나 좋았다고 합니다. 인정받은 만큼 앞으로도 알고리즘 문제해결 커뮤니티에 의미 있는 기여를 할 수 있으면 좋겠습니다.
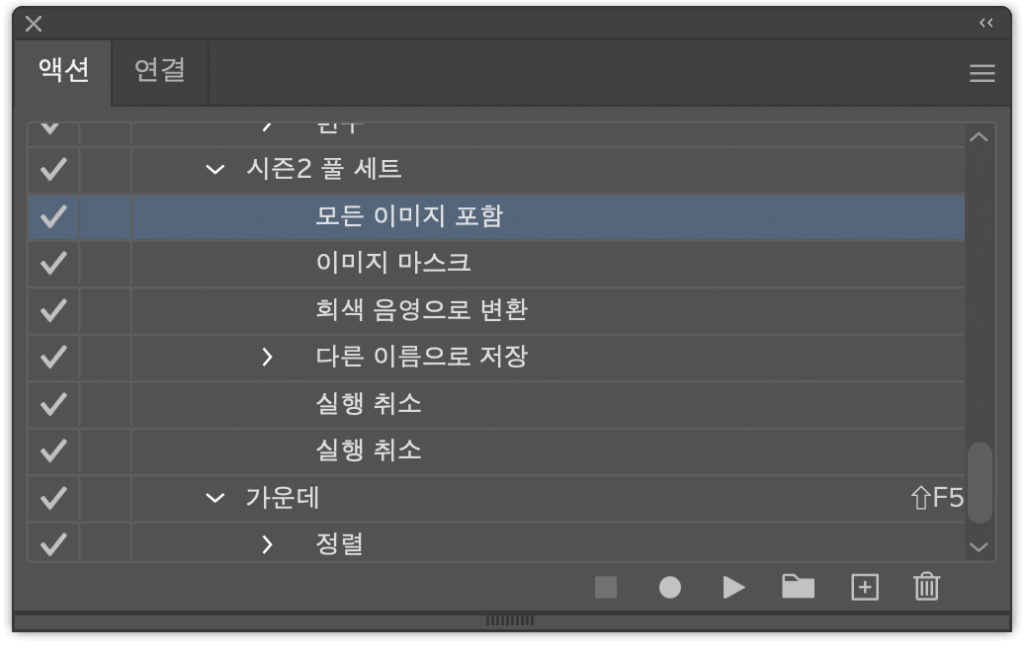
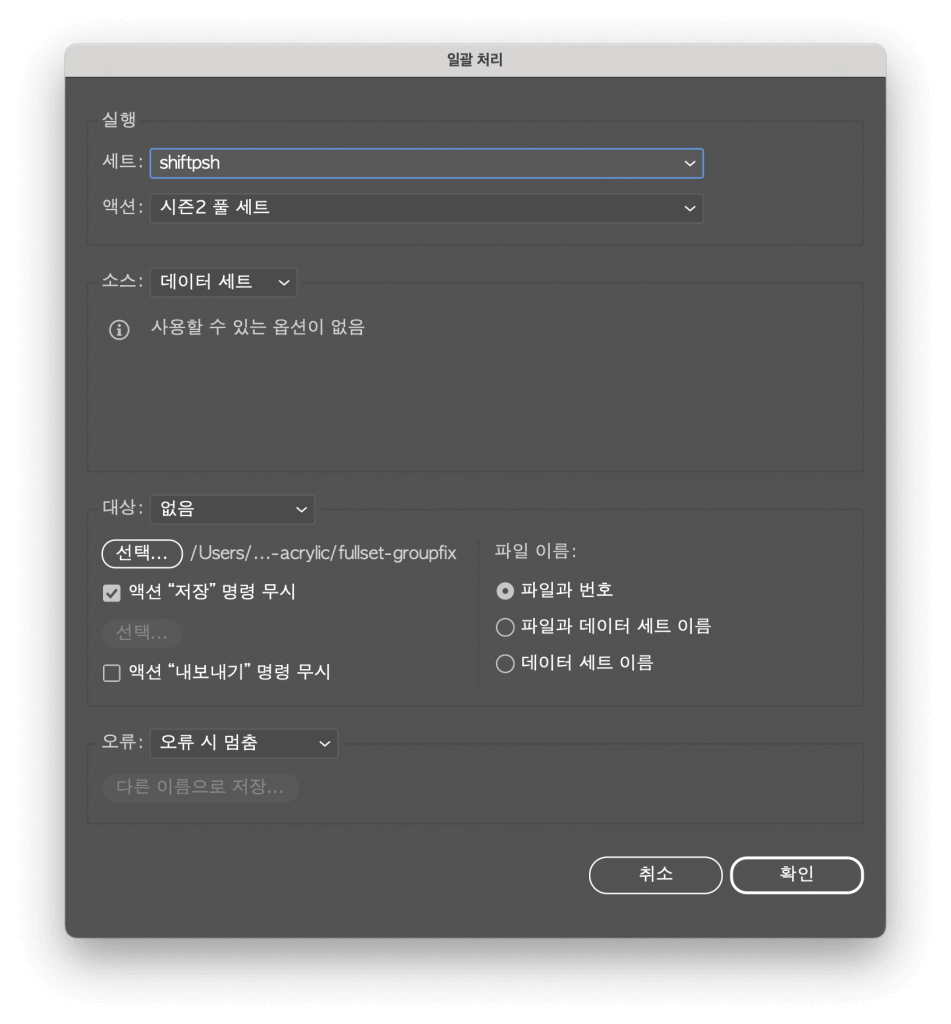
이외에 올해의 솔브드는 대부분 보이지 않는 곳에서 일했습니다. 가령, 관리 콘솔을 새로 만들었습니다. 관리 콘솔은 제가 주로 처리하는 민원(?)들을 좀 더 빠르고 편리하게 처리할 수 있게 해 줘서, 다른 일들에 집중할 수 있었습니다. 가령 프로필 뱃지를 등록하려면
일러스트레이터에서 작업 -> 포토샵에서 $512\times 512$로 리사이징 -> TinyPNG로 용량 최적화 -> S3에 게시 -> URL 나오면 그제서야 솔브드 DB에 등록
을 해야 했는데, 이제는 리사이징, 최적화, 업로드, DB 등록을 한 화면에서 다 해 줍니다.
그리고 사이트 도움말 페이지도 만들었습니다. 이건 좀 늦은 감이 있는 것 같지만 항상 better late than never입니다.
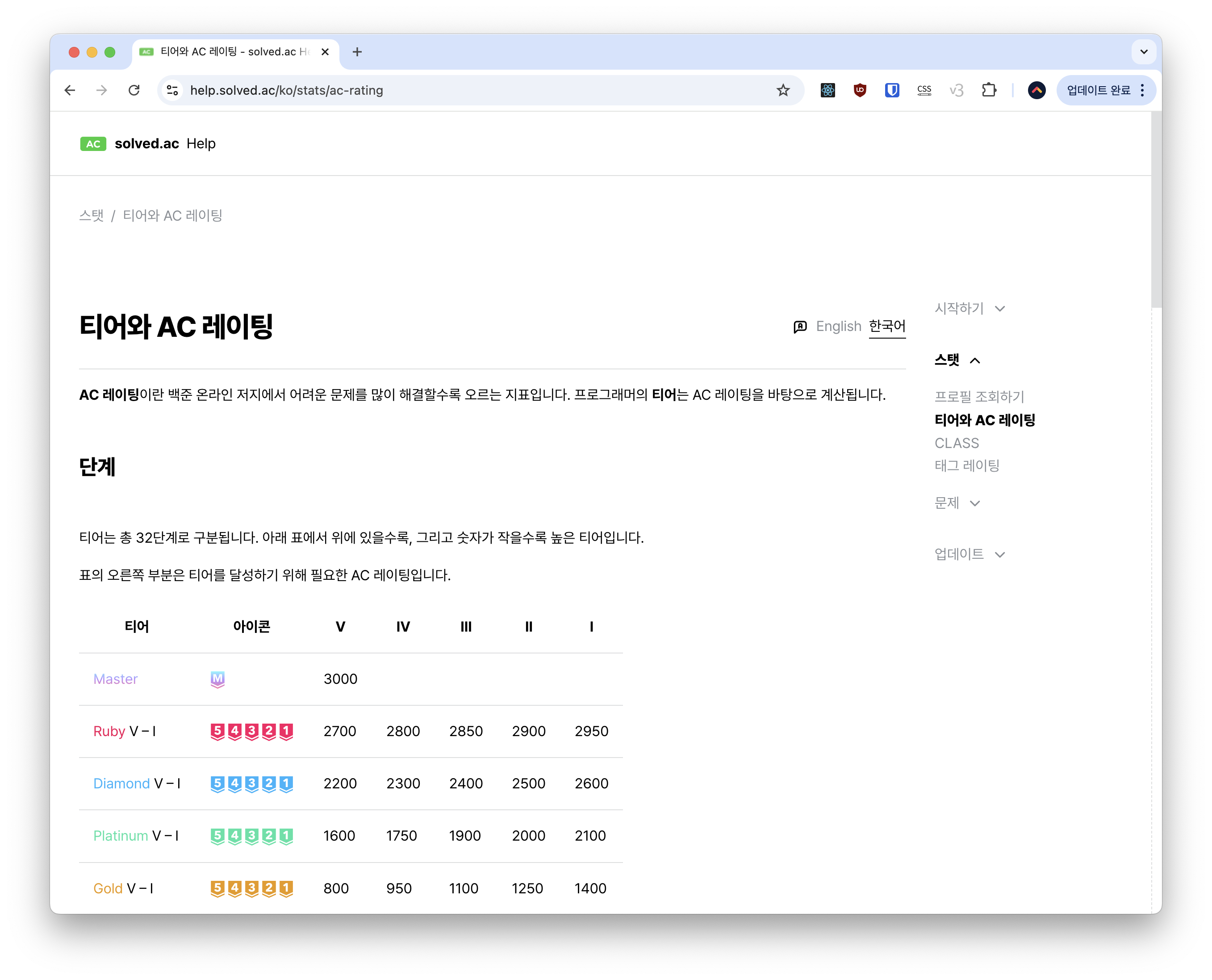
말고도, 신기능 랜덤 마라톤, 프로필 배경 상점, 그리고 문제 오류 제보가 업데이트되었습니다. 길라잡이도 작업에 착수해서 이제 글을 작성하고 있는 단계입니다.
솔브드는 2022년 12월에 회사로 바뀌어서 업력 2년을 맞았습니다. 솔브드의 비전은 그때도 지금도 이렇습니다.
- BOJ에는 정말 많은 문제들이 아카이브되어 있습니다. 이를 잘 체계화해서 알고리즘 문제해결 학습자 및 향유자를 위한 최대의 아카이브 및 커뮤니티로 자리매김하고 싶습니다.
- 알고리즘 문제해결은 사고력과 구현력을 키우는 데에 많은 도움을 주고, 무엇보다도 재밌습니다. 솔브드는 이 분야의 저변을 확대하고, 또한 대중화하고 싶습니다. 특히 코딩 테스트를 준비하던 학습자가 문제해결 자체에도 재미를 붙일 수 있게 하고 싶습니다.
- 한국에는 많은 알고리즘 문제해결 동아리들이 있고, 많은 고등학교/대학교 대회, 심지어 개인 주최 대회까지 꾸준히 많이 열리고 있습니다. 이런 생태계가 최대한 지속 가능하도록 돕고 싶습니다.
이런 것들을 제대로 하기 위해서는 많은 시간이 필요합니다. 솔브드에 쏟을 시간을 확보하려면 다른 일에 쏟을 시간을 줄여야 합니다. 결국 솔브드가 재정적으로 자생 가능해야 한다는 뜻입니다.
2024년 말 기준으로 솔브드는 재정적으로 자생이 가능하기는 합니다만, 저는 재정적으로 자생이 안 됩니다. 뭔가 다른 일을 해서 먹고살아야 합니다. 엎친 데 덮친 격으로 올해 여름에 솔브드 굿즈 샵과 관련해서 결제대행사가 대금을 3개월 늦게 정산하게 된 큰 사고가 있었고, 결제대금을 정산받지 못했기에 굿즈를 (주문해주신 분들께 받은 돈이 아닌) 사비로 발주해야 했던 일이 있었습니다. 큰 규모의 유동성을 잃어서 하반기에는 정말 많이 고생했습니다.
솔브드의 사업화는 학교를 다니는 동안 ‘이걸 평생 할 수 있을까?’를 테스트하기 위한 일종의 실험이었습니다. 실험이 실패했다고 생각하지는 않으나 실험 여건과 기간은 꽤 부족했던 것 같습니다. 여전히 문제해결의 효용과 즐거움을 믿기 때문에 인생이 힘들어진다고 사이트를 닫을 일은 없지만, 제가 의미있다고 생각하는 일을 계속하기 위해서 인생을 갖다가 다이나믹 프로그래밍을 돌리면 이 방향이 제일 옳을 것 같다고 생각해서, 아래와 같이 결정했습니다.
재(?)입사

내년 1월 6일부로 넥슨코리아에서 일하는 것으로 되었습니다. 알고리즘 하고 싶다는 이야기를 하다가 갑자기 게임회사가 나오는 게 좀 의아할 수 있지만 나름의 이유가 있습니다.
첫째로, 제가 가게 될 부서는 오는 1월에 신설되는 다소 실험적인 조직 ‘알고리즘연구팀’입니다. 이곳에서는 사내 코드의 최적화 업무를 할 예정이지만, 주 업무는 놀랍게도 알고리즘 대회 준비입니다.
두 번째로, 저는 넥슨의 사회공헌 사업인 넥슨청소년프로그래밍챌린지(NYPC)의 방향이 제가 솔브드를 만들면서 생각했던 비전과 많은 부분 일치한다고 생각하여, 엔진스튜디오를 퇴사하고도 계속 NYPC 사외에서 문제를 출제하고 자문을 해 왔습니다.
코딩 교육으로 한정하지 않더라도 넥슨의 사회공언 사업에는 진정성이 있다고 생각합니다. 자원과 관심과 의지가 있는 환경에서 제가 의미있다고 생각하는 일을 하는 것만큼 보람찬 것은 없을 겁니다. 물론 이제 회사로서의 솔브드는 정리해야겠지만, 솔브드가 지금 하고 있는 일들도 충분히 의미가 있기 때문에 솔브드가 사라지는 일은 없겠습니다. 개인이 취미로 (하지만 진지하게) 운영하는 사이트였을 때로 돌아갈 뿐입니다.
대회
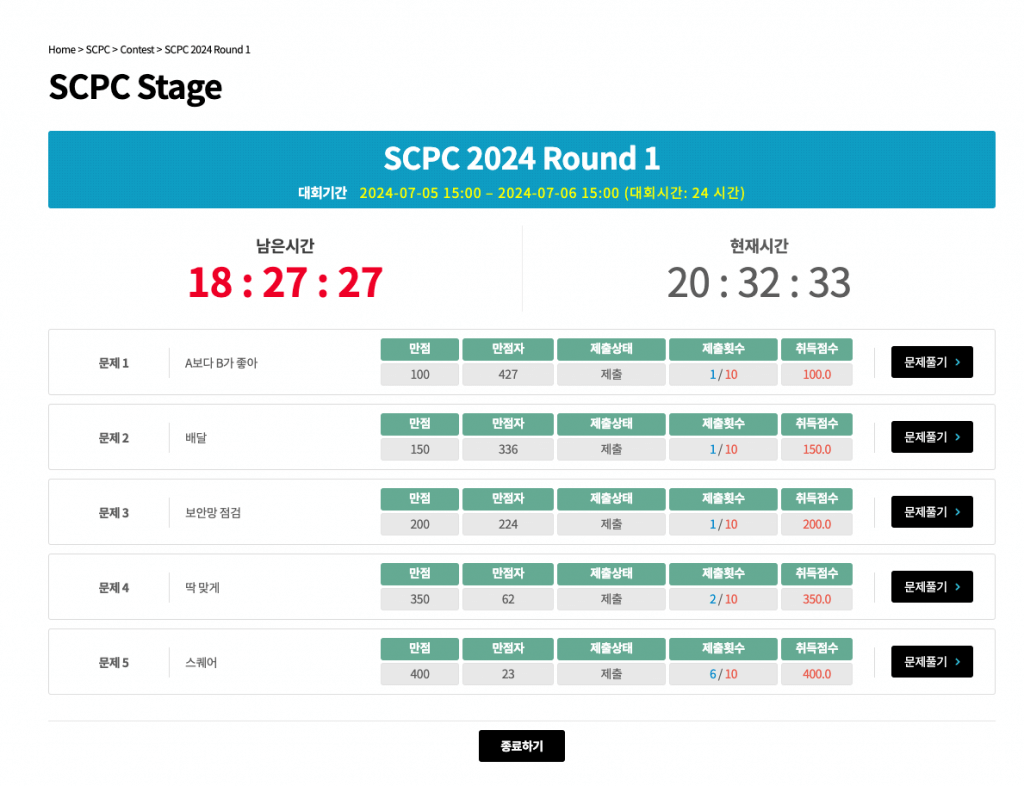
알고리즘 대회를 진지하게 준비하기 시작한 이후 만들었던 버킷 리스트가 있습니다. 여러 번 이야기했던 것 같은데, ICPC 월드 파이널 진출, 코드 잼 라운드 3 진출, 그리고 SCPC(삼성전자 대학생 프로그래밍 대회) 수상이었습니다. 그중 월드 파이널은 2021년에, 코드 잼 라운드 3은 2022년에 이뤘습니다.
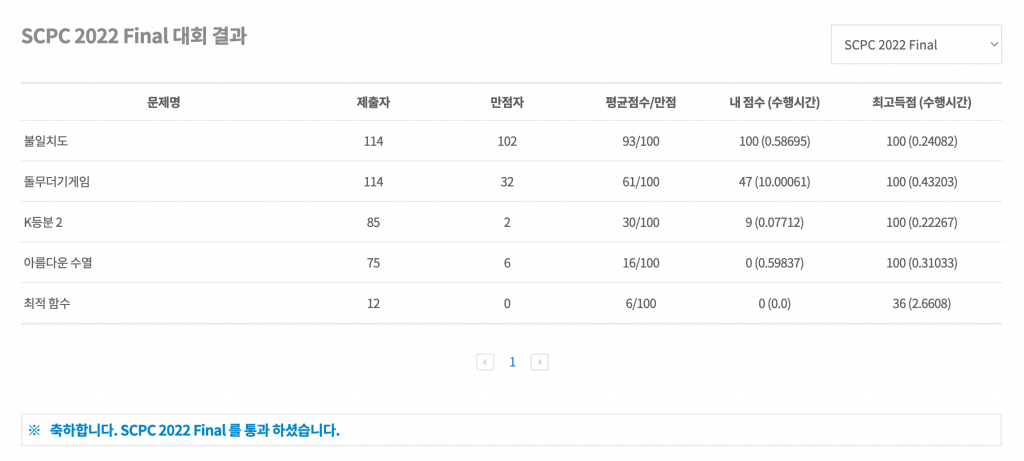
버킷 리스트의 마지막에 있었던 SCPC가 가장 쉬워야 할 터인데, 4번이나 본선에 진출할 동안 여태 상을 못 타다가 마지막 기회인 올해 드디어 수상에 성공했습니다.

그런데 졸업학기라서 그런지 소프트웨어멤버십 가입은 안 시켜 주더라고요. 아쉽습니다.
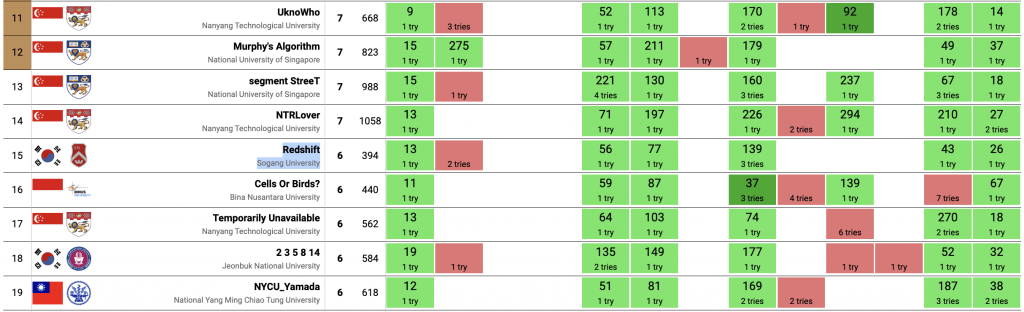
올해에는 ICPC 슈퍼리저널이 신설되었습니다. 그래서 2023-2024 시즌의 첫 슈퍼리저널인 2월 하노이 대회에 참가할 수 있었습니다. 대략 16등까지가 월드 파이널에 진출하는데, 37위로 그렇게 좋은 성적은 아니었습니다. 어려운 평면 그래프 문제를 평면 그래프의 특성을 사용하는 부분 빼고 풀어냈는데, 제대로 하나 배워가는 계기가 되었습니다.

2024-2025 시즌 ICPC 리저널은 서울과 요코하마를 나갈 계획이었는데, 요코하마가 장소 문제로 저희를 등록거부하면서 아쉽게도 서울에만 나가게 되었습니다. 5년만의 수상을 하고 내년 2월 싱가포르에서 열리는 슈퍼리저널 대회로 진출하게 되었습니다. 학교 순위에서 1위를 못 한 건 처음인데, 아쉽기도 하지만 제가 너무 오래 해먹은 것도 맞기 때문에 이제 갈 때가 된 것 같습니다.
돌아보니 관광으로 방문한 지역보다 ICPC에 나가기 위해 방문한 지역이 더 많아진 것 같습니다. 태국, 러시아, 인도네시아, 카자흐스탄, 싱가포르가 있네요.

이외에 UCPC는 팀 ‘개척단 훈련소’로 나가서 4등을 하고 왔는데, B번을 고민하던 기억 말고는 없습니다. 즐겜모드로 나갔으나 저 외의 팀원들이 코드포스 최고 레이팅이 무려 2957과 3042였기 때문에…
취미
shiftpsh.com 사이트를 리뉴얼했습니다. 예전 버전은 shiftpsh.com/2021애서 보실 수 있습니다. 디자인을 훨씬 깔끔하게 만들면서도 더 많은 내용을 넣을 수 있도록 했습니다. 한별이 갤러리도 만들었어요!
2021년도 사이트까지는 제가 2017년에 만들어 뒀던 개인 AWS EC2에다가 FTP 접속해서 pull 받고 빌드 돌리고 그랬는데, 지금은 static generation을 하고 S3에서 호스팅합니다. 소스 코드가 GitHub에 올라와 있습니다. 내년에는 영어 지원을 해 보고 싶네요.

1월에는 작탁을 사서 친구들과 심심할 때마다 마작을 칠 수 있게 되었습니다. 그전에도 마작패는 있었는데, 자동으로 패를 섞는 것의 장점을 실감하게 될 뿐이었습니다.
작탁이 있으니 아카도라와 점봉 같은 걸 추가 구매해서 커스텀 룰도 할 수 있습니다. 가령 5삭/5통 전부 적도라에다가 시로폿치도 있는 3인 마작 같은 걸 할 수 있습니다.

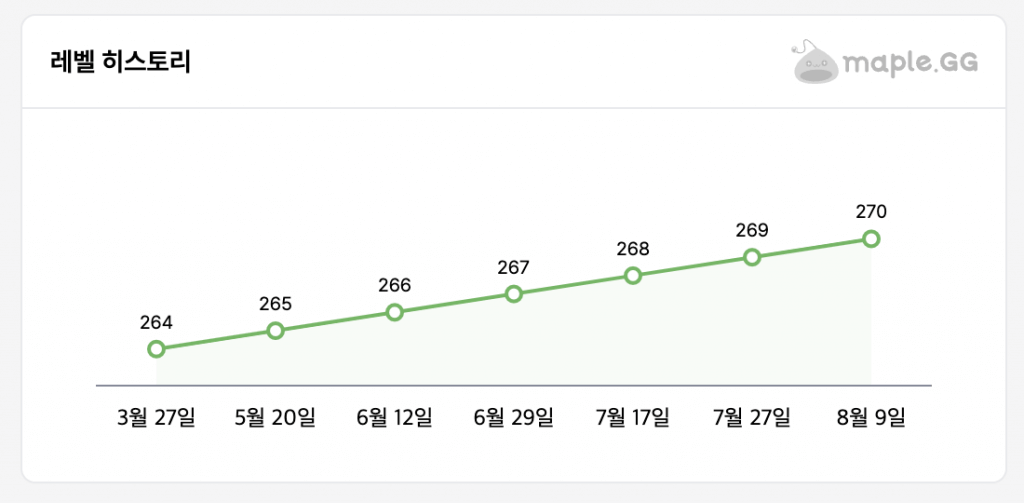
올해로 오락실에 다닌 지 10년째가 됩니다. 10년 중 3년은 유비트를 열심히 했고, 3년은 사볼을 열심히 했고, 최근 4년은 마이마이를 하고 있습니다. DX+ 버전부터 열심히 하기 시작했던 셈이네요. 작년은 레이팅 15545로 마감했는데, 올해는 갑자기 16000을 달성했습니다.
또 예전에 유비트 성과 관리 앱 ‘유비트북’을 만들었던 경험을 살려 마이마이 성과 관리 사이트를 만들기도 했습니다. 제가 필요로 했던 기능들을 잔뜩 넣었더니 참 쓰기 좋은 사이트가 나왔습니다.
츄니즘도 무지개를 달성해서 쌍무지개가 되었습니다. 마이마이 쪽 무지개는 슈퍼 무지개인 것 같기는 한데요.

사볼에 대한 열정은 여전하지 않지만 애정은 여전합니다. 니아·노아 생일 카페의 디자인을 맡았습니다.
여행

2월에는 ICPC를 위해 베트남 하노이에 다녀왔습니다.
베트남이면 동남아시아 국가인데 북쪽이라 그런지 기온이 16도쯤을 유지하고 있어서 꽤나 쾌적했습니다. 롯데호텔에 묵었는데, 1층에 롯데리아와 롯데마크, 그리고 인생네컷이 있어서 잠실인가 싶었습니다.

하노이 탑은 못 봤지만 대신 탑 오브 하노이라는 바를 갔다 왔습니다.
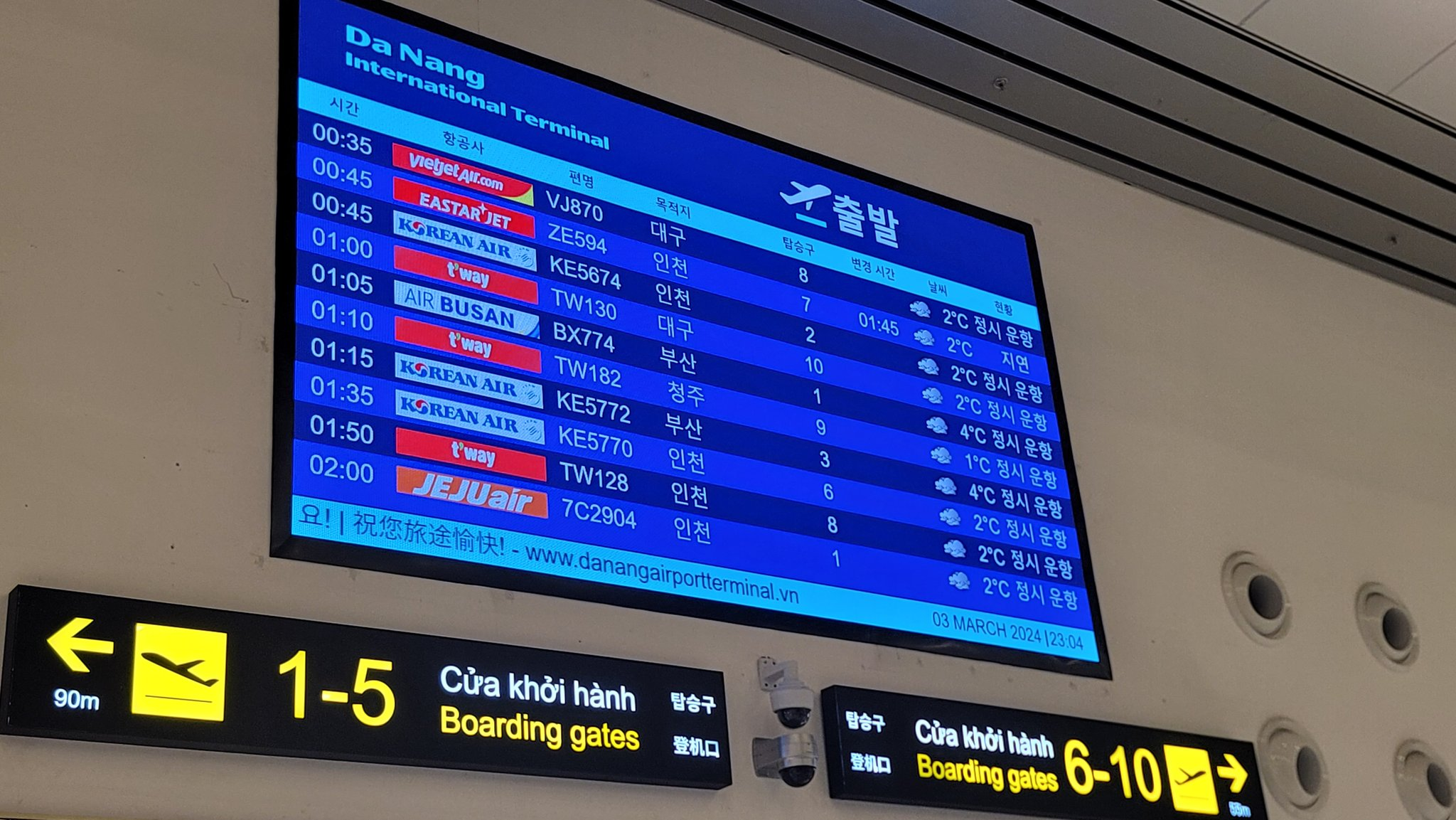
하노이에서 돌아올 때 다낭에서 환승했는데, 마치 한국에 온 것 같았습니다. 세상에 어떤 국제공항이 한국으로 가는 비행기편만 필터해서 보여주는 곳이 있을까요? 정말 신기한 곳이었습니다.

5월에는 일본 후쿠오카에 다녀왔습니다. 순전히 온게키를 하러 가기 위한 여행이었습니다. 그래서 온게키는 재미있었느냐 하면 너무 재미가 있어서 20만원쯤 쓰고 왔던 것 같습니다…


리듬게임에 20만원을 쓸 수 있는 이유는 당연하게도 카드 가챠 시스템이 있어서입니다. 마이마이에 20만원 쓰려면 한 세월 걸리지만 온게키는 10분정도면 할 수 있습니다.


9월에는 ICPC 월드 파이널 발표자로 초청받아서 예정에 없던 카자흐스탄 여행을 떠났습니다. 보통 가는 알마티가 아니라 아스타나였는데, 건물이 큼직큼직한데도 광활해서 놀랐던 기억이 있습니다.
숙소와 비행기 값은 ICPC 재단에서 내 주셨습니다. 감사합니다.

‘ICPC Staff’가 새겨진 티셔츠도 받았습니다. 엄청난 레어템인데 한 번 세탁했더니 글자가 갈라져서 무서워서 못 입고 있습니다. 대신 참가자들에게는 티셔츠를 세 벌씩이나 주기 때문에 같이 간 카이스트 팀 티셔츠 뺏어서 입고 다닙니다.

여기에 마작 세트를 들고 갔더니 마작에 대한 깊은 이해가 있는 일본 참가자들과 국제교류를 이룰 수 있었습니다.

월드 파이널에서도 어김없이 그사건이 일어납니다.

타바스코보다 큰 한별이도 있습니다.
시국

시위도 나갔습니다. 아니 집 앞 바에서 할 거 하고 있는데 갑자기 지인이 와서 계엄령이 났다고 하길래 취한 줄 알았습니다. 지금도 황당합니다. 어쩌다 이런 말도 안 되는 일들이 일어난 걸까요…
탄핵 정국은 현재진행형입니다. 정치는 나의 삶과 지극히 관련이 있다는 걸 한 번 더 체감하게 되는 계기가 되고 있습니다. 대선이 머지않아 있을 것 같은 느낌인데, 이번 일은 잊지 않고 앞으로 계속해서 잘 뽑아야겠습니다.
모닥불을 나서며
올해도 참 힘든 해였습니다. 그렇지만 꽤 멋지고 보람있게 보낸 것 같습니다.
솔브드의 결제대행사 사고는 불가항력적이었고, 이로 인해서 올해 하기로 마음먹었던 것들을 다 하지 못했던 건 아쉬운 일입니다. 회사로 돌아가기로 결정한 건 이런 일의 결과 중 하나지만, 오히려 먹고살 걱정이 해소되면 하고 싶은 일들을 하는 데에 더 집중할 수 있지 않을까 하는 기대도 있습니다.
당장 다음 주부터 회사에 출근하기는 하지만 아직 정비해야 할 것들은 많이 남아 있습니다. 이사를 어디로 가야 할지, 솔브드를 어떻게 정리해야 할지 같은 자잘한 것들도 있지만, 무엇보다 재작년과 작년을 정말 힘들게 보냈는데 잠시 휴식이 필요하겠습니다. 이번 연말은 별 하는 일 없이 요란하지 않게 보내고 있습니다. 새해에도 그렇게 좀 쉬다가, 1월 여행을 다녀오고 나서 본격적으로 모닥불을 나서서 현생을 견디러 나가고자 합니다.
회사를 가게 된다면 프론트엔드 엔지니어를 하러 가게 될 줄 알았는데 그렇지 않게 되었습니다. 하긴 ICPC 월드 파이널에서 발표를 할 줄 알았느냐고 한다면 그것도 모르는 일이었을 터입니다. 삶은 정말 모르는 일의 연속이다 싶습니다. 내년에는 어떤 일들이 저를 기다리고 있을지 기대가 됩니다.
올 한 해도 감사했습니다. 새해 복 많이 받으세요!