UCPC 2020 개최 후기
기회가 되어 올해 전국 대학생 프로그래밍 대회 동아리 연합전대프연 회장을 맡아 UCPC 2020을 개최했습니다. 2019 서강대학교 프로그래밍 대회에 이은 두 번째 대회 운영입니다.
전대프연은 알고리즘 문제해결을 좋아하는 25개 대학교의 26개 동아리의 연합이고, UCPC는 전대프연에서 매년 개최하는 프로그래밍 대회입니다. 보통 가을에 열리는 국제 대학생 프로그래밍 경시대회 한국 리저널의 연습 격 대회로 시작해서, 지금은 국내에서 열리는 프로그래밍 대회 중에서 커뮤니티 대회로는 가장 큰 규모를 갖고 있습니다.
왜 하겠다고 했나요?
대회를 코디네이트하는 건 힘듭니다. 그래서 선뜻 총대를 매겠다고 나서는 경우는 드물고, 실제로 3년 전엔 대회가 안 열린 적도 있었습니다. 4월이 되어도 아무도 대회 총괄을 하려는 사람이 없어 올해는 제가 열어보겠다고 했습니다. 저는 당시 휴학 무직 백수로 즐겁게 하루종일 뒹굴뒹굴 감자칩 먹으면서 매일 컴퓨터랑 눈싸움이나 하고 있었는데, 아마 휴학하고 있지 않았다면 상당히 바빴을 테니 나서지도 않지 않았을까 싶습니다.
인수인계를 받자마자 대회 기획을 시작하고, 출제자를 모집했습니다. 그러나 올해는 큰 문제가 있었습니다. 경우에 따라 기획의 근간이 바뀔 수도 있는 아주 큰 문제였습니다. 바로..
준비되지 않은 우리 앞에 성큼 다가와 버린 코로나 시대

2020년을 살아가는 여러분께서는 모두 마음 속에 우선순위 큐 하나쯤을 갖고 계실 겁니다. 바로 코로나 시대가 끝나면 할 일이라는 이름의 우선순위 큐입니다. 저는 벌써 원소가 120개를 넘어가려고 합니다. 코로나 끝나면 여행 가야지, 코로나 끝나면 맛집 탐방 다녀야지, 코로나 끝나면 못 봤던 친구들 만나서 밥 먹어야지, … 분명 4월즈음에만 해도 큐가 이렇게 커질 거라고는 생각하지 못했습니다. 상황이 괜찮아질 줄 알았으니까요.
UCPC도 마찬가지였습니다. 대회가 열릴 7월즈음에는 상황이 괜찮아지겠지-라는 막연한 기대가 있었습니다. 그래서 오프라인으로 대회를 진행하려고 계획했습니다. 오프라인으로 개최하는 것이 좋은 이유를 나열해 보자면:
- UCPC는 프로그래밍 대회 동아리 회원들의 교류와 경쟁의 장을 목표로 하고 있습니다.
- 부정행위 검사가 힘듭니다. 참가자가 다른 팀 코드를 베꼈는지는 쉽게 알 수 있습니다. 하지만, 예를 들어, 3인 팀 대회인 UCPC에서 4인 이상의 팀원이 코드를 작성한다던가, (진짜 정말 극단적인 예시로) 대회 중에 tourist에게 문제 해법을 물어보고 이를 이용해 해결하는 등의 부정행위는 막기 힘드며 검사하는 것도 거의 불가능에 가깝습니다.
- UCPC와 같은 규모의 대회에는 운영비가 많이 필요합니다. 그래서 스폰서의 도움이 절실합니다. 하지만 온라인으로 진행할 경우 오프라인으로 진행하는 것보다 스폰서에게 후원에 대한 메리트를 어떻게 줄 수 있을지 생각해내고 이를 어필하는 것이 상대적으로 어렵습니다.
반면 온라인으로 개최하는 것도 나름의 장점이 있습니다.
- 예산에서 대관료를 고려할 필요가 없어집니다.
- 대회장에 오지 않아도 됩니다. 지방에서 서울로 올라와서 참가하시는 분들의 경우 대회 참여를 위해 만 하루를 잡고 참가하시는 경우가 흔하다고 들었습니다. 이런 모든 비용을 절감할 수 있습니다.
분명 온라인 대회로 진행해서 얻을 수 있는 장점들도 있지만, 오프라인 대회로 개최하는 것의 장점이 훨씬 크리티컬했기에 할 수만 있다면 오프라인으로 진행하고 싶었습니다.
그러나 모두가 아시는 대로…

…하루 10명대였던 확진 판정은 갑자기 다시 30명, 40명, 80명이 되었고, 오프라인 대회로 개최할 경우 스태프가 방역을 책임질 수 없겠다는 생각이 들어 오프라인 개최를 포기하게 되었습니다.
정작 이 글을 쓰고 있는 시점에서는 일일 확진자가 100명 넘게 발생하고 있네요.
온라인이기 때문에 할 수 있는 것을 하기
그래서 할 수 있는 거라도 최대한 재밌게 해 보기로 했습니다. 일단 위에서 오프라인 대회의 장점으로 언급되었던 것들을 온라인으로 어떻게 살릴 수 있을지에 대해 먼저 고민해 봤습니다.
- 교류와 경쟁의 장 제공 – 기존에 대회장에서 하던 풀이 방송과 스코어보드 방송을 Twitch 온라인 방송을 통해 진행하기로 합니다. 물리적인 공간보다는 덜하겠지만, 실시간 댓글을 통해 교류할 수 있게 됩니다.
- 스폰서 어필 – 온라인 방송 중 방송 화면의 공간을 일부 활용해 스폰서 로고를 지속적으로 노출합니다. 스튜디오가 구해진다면 후원 세션을 참가자들이 가장 많이 볼 시간대인 대회 종료 직후 ~ 문제 해설 전에 진행합니다.
부정행위에 대한 고민이 가장 많았습니다. 대략 다음과 같은 의식의 흐름을 거쳤습니다.
- 웹캠이 있으면 부정행위를 막을 수 있을까?
- 웹캠이 있다고 해도 스크린에 카카오톡 같은 걸 띄우면 충분히 부정행위를 할 수 있지 않을까? 그럼 스크린 녹화도 필요할까?
- 스크린 녹화를 하더라도 다른 장비가 있으면 충분히 부정행위를 할 수 있지 않을까?
- 애초에 참가팀 50팀이 동시 접속할 수 있는 화상 채팅 서비스가 존재할까?
- 존재한다고 하든 안 하든 우리가 그 화면을 전부 모니터링할 수 있는 여력이 있을까?
- 웹캠은 힘들 것 같으니 카피 체크를 하자
- 팀 간의 복붙은 막을 수 있겠지만 4명 이상이 한 팀으로 친 경우는 어떻게 막을 수 있을까?
- 4명 이상이 한 팀으로 치지 않았더라도, 예를 들어 누군가 대회 중에 대회 문제를 random Codeforces red한테 물어봐서 푼다면? 어떻게 막을 수 있을까?
- 그 코드는 언제 다 읽을까?
- 결국 어떻게 해도 부정행위를 막을 수는 없는 거 아닌가?
- 근데 어차피 부정행위 해서 높은 점수 받고 못 보던 사람이 스코어보드 위에 있는 상황이 발생하면 다 티나지 않을까?
결론은 PS 커뮤니티를 믿고 코드 카피 체크 이외의 별도의 부정행위 검사를 하지 않는 것으로 났습니다. 커뮤니티 대회였기에 가능했던 결정이었습니다. 큰 상금이 걸린 기업 대회였다면 이런 상황에서 상당히 곤란했을 것입니다.
인터넷 방송

그렇게 결정하고 나니 인터넷 방송이 대회 기획에서 출제와 검수를 제외한 가장 중요한 요소가 되었습니다. 프로그래밍 대회에 많이 참여해 보셨고 (무려 ICPC 월드 파이널!) 관련 스트림도 자주 하시는, 세계적인 인기를 자랑하는 월클(World Class) 스타 정재헌Gravekper님께 참여해주실 수 있는지 여쭸고, 흔쾌히 승낙해 주셔서 함께 온라인 방송을 기획하게 되었습니다.
방송에서 뭘 다루면 좋을지, 방송을 언제부터 켜면 좋을지, 화면은 어떻게 구성하면 좋을지 등등을 대회 직전까지 열심히 논의했습니다. 인터넷 방송에는 문제 풀이, 스코어보드, 후원 세션은 필수로 들어가야 했고, 이외에 대회에 참여하는 사람들도, 참여하지 않는 사람들도 모두 볼 수 있다는 점을 감안하면서 대회 종료 전에 뭘 하면 좋을까를 고민했습니다. 이에 온라인 방송이 있는 다른 대회들을 참고했습니다.
- ICPC나 IOI는 대회 중에 실시간 스코어보드와 문제 해설을 보여줍니다. ICPC 방송은 생각보다 재밌습니다. 그래서 사실 제가 하고 싶었던 이상에 가까웠던 방송 형태이긴 하나, 온라인 대회이고 웹캠 사용을 포기했기 때문에 화면에 보여줄 수 있는 게 없었고, UCPC 방송은 대회 참가자들도 볼 수 있는 방송이었기에 문제 해설도 보여줄 수 없었습니다.
- 반면 Google Hash Code 방송은 참가자들이 대회 중에 시청할 수 있습니다. 그래서 대회 시작 전후에만 방송을 하고, 대회 중에는 아무것도 보여주지 않습니다.
하지만 대회 중에 아무것도 보여주지 않으면 심심하기 때문에 간단히 스코어보드를 띄워 두기로 결정했습니다.
문제 풀이와 후원 세션도 걱정이었습니다. 지금까지 UCPC 풀이는 출제자가 강단에 나와 슬라이드를 보여주는 식으로 진행했고, 후원 세션도 마찬가지였습니다. 근데 올해는 어쩌죠?
다행히 감사하게도 작년에 이어 고려대학교 SW중심대학사업단에서 장소를 제공해 주셔서, 고려대학교 정보대학의 대형 강의실 하나를 스튜디오로 사용할 수 있었습니다. 기존처럼 출제진이 강단에서 슬라이드로 발표하고 이를 카메라로 찍어 방송할 수 있었습니다.
출제와 검수
코로나 시대가 되어도 프로그래밍 대회에서 변하지 않는 것은 바로 출제와 검수입니다. 올해는 제가 여름에 회사에 갈 걸 우려해 대회 준비를 일찍 시작했습니다. 출제진은 우리나라 최대의 알고리즘 문제해결 커뮤니티인 BOJ Slack에서 모집했고, 이후에 추가로 call for tasks를 통해 문제 공모를 받았습니다. 올해는 공모받은 문제가 많아 출제진 풀이 상당히 컸습니다.

기획을 포함해 모든 소통은 Slack으로 진행했습니다. Slack의 (무료 버전의) 최대 단점은 메시지가 10,000개 이상 쌓이면 이전 메시지들은 하나씩 못 보게 된다는 것인데요, 마침 코로나로 인해 Slack에서 3달간 무료로 Standard Plan을 제공해 주고 있어서 고민 없이 사용했습니다.
문제마다 하나의 채널을 만들어 최대한 맥락을 잃지 않고 대화할 수 있도록 했습니다. 또한 대회 전반적인 공지를 올릴 #general 채널, 인터넷 방송을 기획할 #broadcasting 채널, 컨테스트 도중 생기는 라이브 이슈에 대응할 #contest-finals / #contest-preliminaries 채널 등을 필요에 따라 주제 단위로 만들어 활용했습니다.

특히 박수찬tncks0121님의 도움을 받아, Slack과 Zapier 연동을 사용해 call for tasks로 메일을 받으면 메일 내용을 자동으로 Slack 채널에 포워딩해 주도록 설정할 수 있었습니다. 다만 Zapier의 문제인지 후술할 UCPC 메일서버 문제인지는 모르겠지만 메일이 몇 개 누락되는 경우가 생겼습니다. 이런 경우엔 제가 UCPC 메일함에서 직접 공모받은 문제를 출제 채널에 배달해야 했습니다.

출제/검수 현황과 문제 자료 관리 등에는 Google Drive를 사용했습니다. G Suite에 제공되는 기능인 공유 드라이브를 적극적으로 활용했습니다.
출제
대회 분위기 정하기
출제 초기에는 예선과 본선 각각의 적절한 난이도 커브를 결정해 주는 것이 중요합니다. 문제들이 너무 쉬우면 대회 중에 문제를 전부 해결하는 팀은 대회가 끝날 때까지 할 게 없어서 심심해지고, 반대로 너무 어려우면 문제들에 압도당한 팀들이 좌절하게 되기 때문입니다. 그래서 먼저 난이도 커브를 정하고, 이에 맞춰서 어떤 문제를 내야 할지, 문제 풀에서 어떤 문제는 사용하고 어떤 문제는 사용하지 말아야 할지 등을 결정할 수 있습니다. 작년 서강대 대회 출제 후기에서 언급했던 것이기도 합니다.

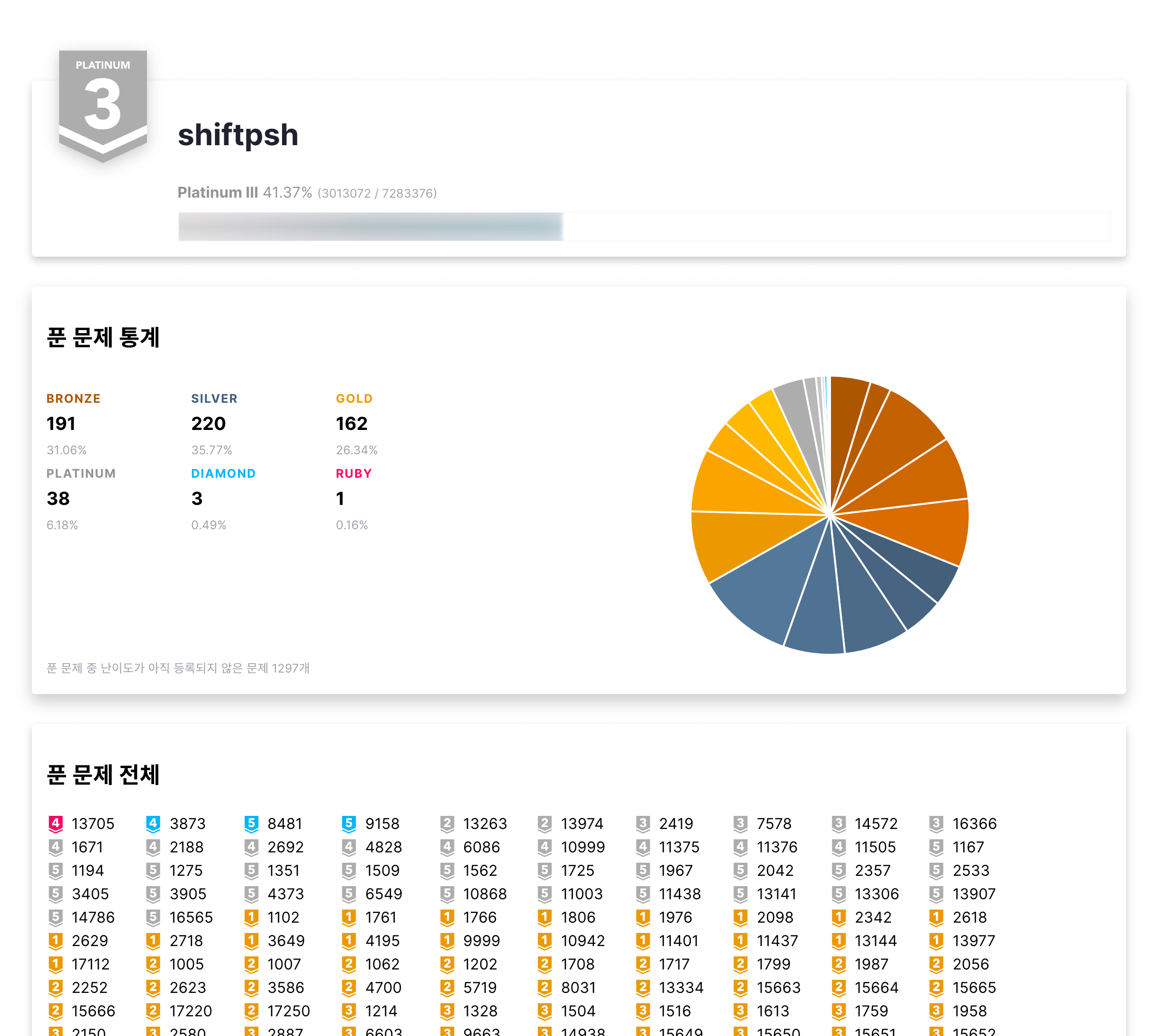
이와 관련해 작년 UCPC와 올해 UCPC의 가장 큰 차이는 문제의 난이도를 가늠할 수 있는 수단인 solved.ac의 존재였습니다. 서울 리저널의 난이도 분포를 참고해서 문제 풀에 있는 문제들의 난이도들을 각자 가늠해 보고, 예선과 본선 중 어느 쪽에 사용할지 플로우를 잘 돌렸습니다. 또한 시트에 추가적으로 알고리즘 분류를 적어 넣어, 한 분야에 너무 치우친 컨테스트가 되지 않도록 문제 배치를 잘 해주었습니다. 다만 검수 과정에서 난이도와 분류 정보를 보는 것은검수에 악영향을 끼칠 수 있어서 해당 시트는 출제진만이 편집했고, 검수 현황 시트를 따로 만들어 두었습니다.

Call for tasks로 공모받은 문제들도 이렇게 출제진끼리 난이도를 가늠해 보고 대회에 필요하리라 생각된 문제들을 채용했습니다. 공모받은 문제들과 내부에서 출제한 문제들이 많아서 아쉽게도 사용할 수 없게 된 문제가 많았습니다.
디스크립션과 데이터 작성

데이터의 무결성을 최대한 보장하기 위해 디스크립션 작성을 제외한 모든 작업은 Polygon에서 testlib을 사용해 진행했습니다. Polygon 서버가 다소 불안정해서 조마조마한 상황이 몇 번 있었고, 패키지 전체를 자주 백업했습니다.

문제지는 solved.ac 서버에 올라가 있는 비밀의 시크릿 프린세스 self-hosted Overleaf에서 작업했습니다.
디스크립션과 데이터 작성에 있어서는 대회 참가자가 문제 디스크립션을 이해하거나 기타 문제에서 중요하지 않다고 생각되는 이슈들을 해결하는 데 시간을 소비하지 않도록 하게 하기 위해 다음 원칙에 따라 UCPC 출제 컨벤션을 만들고 이를 최대한 지키려 노력했습니다.
- 일부러 디스크립션을 이해하기 어렵게 하는 컨셉의 문제가 아닌 경우, 디스크립션은 한 번만 읽어도 이해할 수 있을 정도로 이해하기 쉬워야 하며, 디스크립션이 문제 해결을 방해해선 안 됩니다.
- 같은 맥락에서 어려운 수학 기호 및 개념은 가능할 경우 최대한 사용하지 않습니다. 갓 고등학교를 졸업한 사람이 봐도 이해할 수 있는 수준이어야 합니다. 이를테면, ‘$A$의 모든 원소들의 제곱의 합’이라고 적을 수 있는 것을 굳이 ‘$\sum_{a\in A} a^2$’라고 적지 않습니다.
- 글과 문자가 쉽게 구분되면서 문자가 글을 읽는 데 방해가 되는 일이 없도록 해야 합니다. 따라서 모든 문자는 기울임꼴로 작성하고, 수식에는 띄어쓰기를 잘 하며, 기호는 정확한 것을 사용해야 합니다.
- 입출력 변수의 범위는 입출력 섹션에 한꺼번에 명시하는 것이 가장 좋습니다.
- 데이터는 무결해야 합니다. 명시한 형식과 다른 데이터가 있어서는 안 되며, 입력 데이터에 대한 정답이 아닌 데이터가 출력 데이터로 되어 있어서는 안 됩니다.
- 생소한 입출력 방법 등으로 참가자가 고생하는 일이 없어야 합니다. 특히 EOF로 출력의 끝을 명시하는 입력 데이터들이 그렇습니다.
또한 디스크립션을 굳이 Polygon에서 작업하지 않은 이유가 있다면, BOJ의 문제 출제 플랫폼인 BOJ Stack의 존재 때문입니다. BOJ에서 대회를 개최하기 때문에 대회 전에 문제들을 전부 BOJ로 옮겨야 하는데요, 대회 직전에는 디스크립션 수정이 잦습니다. 근데 Polygon에서 디스크립션을 관리하게 되면 어차피 만들어야 하는 문제지에서도 디스크립션을 수정해야 하고, BOJ Stack에서도 디스크립션을 수정해야 합니다. 또한 BOJ Stack에서는 LaTeX을 최대한 쓰지 말아달라고 하기 때문에 TeX로 작성한 문제들을 전부 HTML로, 이를테면 $1 \leq N, M \leq 200\ 000$ $1 \leq N, M \leq 200\ 000$과 같은 식은 1 ≤ N, M ≤ 200 1 ≤ <em>N</em>, <em>M</em> ≤ 200 000으로 다시 포맷해야 하는데, 이는 생각보다 상당히 고통스럽습니다. 이런 공수를 줄이고자 Overleaf에서만 디스크립션을 관리했습니다.
물론 HTML로 포맷하는 공수조차 줄이고자 그냥 모든 문제에 TeX을 사용했습니다. 이렇게 할 경우 Overleaf에서 Stack으로 문제 본문을 복사+붙여넣기 하면 세팅이 끝납니다. 참 쉽죠.

문제와 해설에 사용될 그림의 경우, 그림을 요청하는 채널을 따로 만들어서 출제진의 요청을 받고 제가 그림을 열심히 제작했습니다.
마지막으로 정해는 ICPC 경향에 맞춰 C++과 Kotlin(또는 Java)으로 모두 작성했고, 해당 언어들로 문제를 해결 가능함을 보장했습니다.
검수
문제 초안이 완성되면, 문제를 검증하게 됩니다. 주로 다음과 같은 항목들을 검증해야 합니다.
- 데이터와 디스크립션의 포매팅이 올바르고well-formed 무결한지 (UCPC 컨벤션을 지키는지)
- 출제자의 풀이가 완벽한지
- 출제자가 의도하지 않은 풀이로 풀리지는 않는지, 출제자가 의도하지 않은 풀이로 풀렸다면 그 풀이도 정답으로 허용할 것인지
검수진은 바로 위와 같은 항목들을 꼼꼼히 확인하는 역할을 합니다. 출제진들 사이의 교차 검수crosschecking 이외에도 외부 검수진을 모셔 와 검수를 진행했습니다.

참가팀들이 틀린 방법으로 접근할 것 같은 풀이(‘사풀이’라고도 합니다)를 미리 예상하고, 이를 적절히 막습니다. 방법은 여러 가지입니다. 예를 들어,
- 어떤 자연수 $N$이 소수인지 판별해야 하는 문제에서, $N=1$이 입력으로 들어오는 경우를 제대로 처리하지 못하는 코드들을 틀리게 하기 위해 $N=1$인 데이터를 준비할 수 있습니다. (예외 처리 데이터)
- 혹시라도 고려하지 못한 경우가 있을 수 있으니 랜덤에 의존해 제작한 일반적인 데이터를 추가로 더 준비할 수 있습니다.
- 아예 틀린 방법으로 문제를 해결하는 코드가 준비한 데이터를 운좋게 전부 통과하는 경우가 있다면, 틀린 방법으로 풀면 틀리거나 시간 초과를 받는 데이터를 준비할 수 있습니다. (반례 데이터)
- 출제자가 의도한 풀이보다 훨씬 쉬운 풀이로 풀리는 경우 시간 제한을 조정하거나 문제에 등장하는 상수들의 제한을 조정할 수도 있습니다. 의도한 풀이로 접근하면 풀리지만 의도하지 않은 풀이로 접근하면 시간 초과를 받도록 적절히 제한을 조정합니다.
등과 같은 과정을 거쳐 문제를 완벽하게 만들었습니다.
다들 모여

재작년과 작년의 참가 조건이 마음에 들었고, 그대로 유지했습니다. 석박통합과정 학생의 참가 조건만 명확하게 정했습니다.
- 3명이 1개 팀으로 참가해야 함
- 학부생이라면 재학과 휴학을 불문하고 참가 가능
- 대학원생이라면 석사과정 또는 석박통합 2년차까지 참가 가능
- 다른 학교 구성원끼리 팀을 이루어 참가 가능
수상 경력에 따라 제한 조건을 둘까도 생각해 봤는데, UCPC는 역시 한국 최강자전의 컨셉인 것도 있는 것 같아 딱히 두지 않았습니다. 총 299팀이 예선대회에 참가를 신청해 주셨습니다.
매년 하던 것처럼 Google Forms를 이용해 참가 신청을 받고 GMail을 통해 공지사항을 전송했는데, 대회 규모가 커지면서 이 방법을 계속 사용하기엔 다소 무리가 있는 것 같다는 생각을 했습니다.
- 참가자 중 메일 주소에 오타를 낸 참가자들이 몇몇 계셨습니다. 실제 예시로, nvaer.comnaver.com, gamil.comgmail.com, kaist.co.krkaist.ac.kr 등으로 도메인에 오타를 낸 메일 주소들을 확인할 수 있었고, 제 수작업으로 고쳤습니다. 도메인 오타는 어찌저찌 고칠 수 있는데 @ 앞 부분에는 과연 오타가 없었을까요? 이메일 인증에 기반한 서비스를 사용하거나, 이를 직접 구현해야겠다고 느꼈습니다.
- 예선 계정 정보 메일 299개를 하나하나 작성해 보냈습니다. 또한 GMail에 일일 전송 메일 수 제한이 있다는 사실을 이 대회 운영하면서 처음 알았습니다. 이 때 대량 자동 메일 전송 시스템을 구축했어야 했는데, 그러지 못했던 것이 후술할 예선대회 대참사로 이어집니다.
예산 확보

출제자 분들과 검수자 분들께 노력에 대한 합당한 대우를 드리고, 참가자 분들께 상을 드릴 수 있도록 예산을 정했습니다. 온라인 대회였기 때문에 장소나 비품, 식사 등에 대한 고려는 할 필요가 없다고 생각했으나.. 오산이었습니다. 온라인 방송을 할 장소와 장비가 필요했고, 상품이 있다면 상품을 배송할 비용도 필요했습니다. 대관료와 장비, 배송비 등을 종합해 보니 온사이트로 치뤄진 예년 예산만큼은 못해도 상당히 무거운 예산이 나왔습니다.
감사하게도 대회를 열겠다고 하자마자 케니소프트, 알고스팟, 스타트링크, 그리고 고려대학교 SW중심대학사업단에서 후원 의사를 보내 주셨습니다. 이후에도 여러 개발 기업에 무작정 메일을 보냈고(…) 마인즈랩과 네이버 D2에서 출제와 검수 비용을 지원해 주셨습니다. 대단히 감사합니다! (solved.ac의 경우 사실상 제 개인 후원이기 때문에 논외로 합니다)
온라인 대회여서 기존의 후원 세션을 기존처럼 진행할 수 없어 어떻게 어필할 수 있을까 고민했습니다만, 오히려 온라인 대회이고 공개된 온라인 방송으로 대회를 진행하기 때문에 굳이 참가자가 아니더라도 대회 방송을 볼 수 있고, 따라서 알고리즘 문제해결에 대한 충분한 관심이 있는 시청자들에게 기업을 홍보할 수 있다는 점을 어필하기로 했습니다.
사실 출제와 검수는 이전에 서강대 대회를 총괄해 본 적이 있었기에 어느 정도 익숙한 부분이었습니다. 하지만 서강대 대회는 학과 사업이어서 후원사를 구할 필요가 없었던 반면 UCPC의 경우에는 우여곡절이 많았고, 실수도 했습니다.
가장 큰 실수는 후원 조건을 명확하게 정하지 못했고, 또 이를 후원사에 제대로 공유하지 못했던 것이었습니다. UCPC에서는 홍보 기업 발표 세션을 진행하는데, 온라인 방송으로 홍보 세션을 진행하면 참가자들이 도중에 방송을 이탈해 효과가 반감될 것을 우려하여 후원 조건 금액을 높게 정했습니다. 그러나 죄송하게도 다른 바쁜 일들에 정신이 팔린 제 불찰로 인해 이를 공유받지 못한 후원사가 계셨습니다. 다음 대회부터는 이번 일을 반면교사로 삼고, 가능하다면 파이콘의 예처럼 후원 조건을 합당하고 명확하게 정하고 홈페이지에 공지하며 후원사와 긴밀히 소통할 수 있도록 해야겠습니다.
후원 기업들에 다시 한 번 무한한 감사를 드립니다.
예선 방송 리허설(7월 23일): 폭풍전야
대회 전에 리허설을 통해 방송 진행 계획을 구체화했습니다. 운영진들과 함께 안암의 명물 고고 인디안 쿠진에서 카레를 먹고, 대회 중 스튜디오로 사용될 고려대학교 정보대학 강의실에 숭고한 연합대회가 진행되는 도중 급습해 모여 강의실의 배치와 장비 등을 확인하고, 인터넷 속도는 방송을 송출하기에 충분한지, 강의실 구조 상 풀이 and/or 후원 세션은 어떻게 하면 좋을지 논의했습니다. 관련해서는 가장 고민을 많이 하신 재헌님의 UCPC 2020 방송 후기를 참고하시면 좋습니다.
OBS가 브라우저 화면을 겹쳐 띄워 둘 수 있다는 것을 이용해 기획한 대로 제가 대회 직전(당일 새벽 3시까지!)에 React로 간단하게 방송 씬을 만들었습니다. 코드는 여기 올라와 있습니다.
예선(7월 25일): 이 곳이 어둠의 기운으로 가득차 곧 무슨 일이 일어날 듯 합니다

방송 씬을 만드느라 날을 새고 10시에 고려대에 도착해서 세팅을 시작했습니다. 운영진들은 과연 올솔이 몇 팀이나 나오고 언제 제일 먼저 나올까 내기를 합니다.
막상 대회 시간이 다가오니까 대회 진행 플랫폼인 BOJ가 500 Internal Server Error와 502 Bad Gateway 에러를 뱉기 시작합니다. 어…? 이대로는 대회를 정상적으로 진행할 수 없겠다 싶어 대회 시작을 14:10으로 10분 연기했습니다.
그런데 좀 잠잠해지나 싶더니 14:07쯤 되니까 같은 현상이 다시 일어나는 거였습니다. 10분을 더 연기할까 고민하고 있던 찰나, BOJ Stack도 먹통이 되었습니다. 대회 정보는 BOJ Stack이라는 관리 페이지에서 수정해야 합니다. BOJ Stack이 접속이 막히면 운영진도 대회 시간을 수정할 수 없습니다.

’14:20에는 괜찮아지겠지? 그럼 종료 시간을 10분쯤 연장해야겠다’고 생각했습니다. 서버는 비웃기라도 하듯 계속 접속을 거부했습니다.그런 와중에 UCPC 관련 메일 아래에 적혀 있던 제 전화번호로 참가팀들의 전화가 걸려오기 시작했습니다. 운영진도 대회 서버에 접속할 수 없는 상황임을 알려 드렸습니다.
이제는 대회를 어떻게 할지 빠르고 공정하게 결정해야 했습니다. 특히 여러 지역에서 모여서 대회를 치기 위해 스터디룸을 빌리는 팀이 많다고 알고 있어, 이 분들의 피해가 최소화되도록 하려면 어떻게 해야 하나 고민했습니다. 그 와중에 대회 사이트에서 문제 제목을 읽은 팀이 있다는 제보를 받았습니다. 문제 제목을 읽은 팀이 있었다는 것은 문제를 읽은 팀이 있었을 수 있다는 뜻도 되므로 신중하게 결정해야 했습니다.
정말 다행히도 이번 UCPC는 온라인 대회였기에 공간의 제약을 받지 않았고, 본선에 몇 팀이 출전하더라도 수용할 수 있었습니다. 그래서 아예 기업 대회 Qualification 라운드의 형식으로 본선 커트라인을 명시하고 시간을 대폭 연장하기로 결정합니다. 그리고 단체 메일을 보냈습니다.


그런데, 감사하게도, 구글이 제가 아이패드(구글 계정 입장에서는 ‘새로운 기기’)로 대량의 메일을 보내려는 시도를 감지하고 전대프연 계정을 차단시켰습니다. 제가 회장이 되면서 바꾼 비밀번호로는 로그인이 안 됐고 이전 비밀번호로 인증을 받아야 했는데, 무려 제 전전전임 회장께서 설정하신 비밀번호였습니다. 당장 연락을 드렸지만 회신을 무작정 기다릴 수도 없는 상황이었어서, 제 개인 메일으로 단체 공지와 문제지를 전송했습니다. 이 때가 오후 3시였습니다.
서버 상황은 오후 4시를 즈음하여 개선되었고 코드를 제출할 수 있는 상황이 되었습니다. 예선대회에서도 해설과 스코어보드 공개를 할 예정이었고, 이를 위해 출제진들이 모여 있었으나, 안타깝게도 이후 방송은 진행하지 못했습니다. 여러모로 아쉬웠습니다. 예선 당일 서버 사고가 일어났던 이유는 여기에서 읽을 수 있습니다.

결과적으로 본선 진출 팀은 총 170팀이 되었고 의도치 않게 역대 최대 규모의 본선이 되었습니다. 컷을 5문제로 잡았으면 좋았겠다는 의견도 많았으나 안타깝게도 결정 당시에는 출전 팀들의 실력을 가늠하기 힘들었습니다.
본선도 규모가 예선 못지않게 커져버렸고, 본선대회에서도 같은 일이 되풀이되면 안 되었기에 만반의 준비를 했습니다. 우선 스타트링크와 함께 이런 일이 일어난 원인을 분석하고 당시 일어났던 상황이 재발되지 않게 하기 위한 기술적 조치를 취했습니다. 본선도 BOJ에서 치루는 것으로 결정했으나, 혹시 모를 사태에 대비하기 위해 UCPC 운영진도 DOMjudge 서버를 직접 구축해 대비했습니다.
본선(8월 1일):

정말 다행이게도 본선대회는 아무 문제 없이 순조롭게 잘 진행되었습니다.
서버 대비와 별개로 본선대회를 위해 준비한 것들이 몇 개 더 있었습니다. 그 중 가장 눈여겨볼만했던 건, 대회 중에도 공지했던 바 있지만, 이번 UCPC는 스코어보드 공개의 재미를 위해 프리즈 기준을 다소 특이하게 잡았던 것이었습니다.
프리즈 시간은 대회 종료 60분 전이었으나, 프리즈 시간과 관계없이 어떤 팀이 9문제를 해결한 순간 이후 그 팀의 모든 제출이 비공개되는 식이었습니다. 이를 위해 BOJ에서 스코어보드를 제공하지 않고 scoreboard.ucpc.me라는 별도의 사이트에 스코어보드를 띄웠습니다. 박수찬tncks0121님께서 운영자 스코어보드의 모든 제출을 $n$초마다 가져와서 가릴 건 가리고 공개 스코어보드에 보여주는 파이썬 스크립트를 짜 주셔서 가능했던 일이었습니다.
풀이는 원래 라이브로 방송하려 했으나, 풀이 슬라이드가 대회 중에 완성되기도 했고, 진행을 비교적 여유롭게 하기 위해 녹화방송으로 바꿔 진행했습니다. 풀이 슬라이드가 방송에서 사용한 것과 공개된 것이 다른데, 방송에서의 풀이 슬라이드는 출제진이 생각한 난이도 순서대로 문제가 정렬되어 있고, 공개된 풀이 슬라이드는 A, B, C.. 순입니다. 특별한 이유가 있다면 공개 슬라이드에서는 풀이가 필요한 문제를 더 빨리 찾게 하기 위함이었습니다.
본선대회를 성공적으로 종료하고 저를 제외한 운영진은 고기를 맛있게 먹으러 갔다고 합니다. 저는 안타깝게도 당일 너무 피로해서 그냥 집에 와서 곯아떨어졌습니다. 비극적인 엔딩이네요.
어땠나
힘들지만 의미있는 경험이었다고 말하면 식상할까요?
힘들었던 것들
전대프연 회장을 하는 것은 힘든 일이라고 익히 들어서 알고 있었지만 구체적으로 어떤 게 힘든 일인지는 잘 몰랐습니다. 이제 대략 알게 되었습니다.
- 후원사를 구하기가 상당히 힘들었습니다. 온라인이어서 더 그랬습니다. 올해 ICPC도 후원 사정이 좋지 않다는 걸 생각하면 어디나 비슷한 것 같습니다. 그래서 개인적으로 옆 나라 리저널의 후원 사정이 꽤 부러웠습니다.
- 상금 처리라던가 참가 상품을 택배로 보내야 했던 것도 힘든 점 중 하나였습니다.
- 6월 말에 넥슨코리아 엔진스튜디오에 산업기능요원으로 입사하게 되었습니다. 6월까진 무직 백수여서 몰랐는데, 대회 코디네이팅과 왕복 3시간의 출퇴근 생활을 병행하는 것은 체력적으로 상당히 힘든 일이었습니다. 회식 도중에 나와서 대회 개최를 준비했던 적도 있습니다.
- 이외에는, 참가자 등록이 번거로웠습니다. 특히 재학증명서와 휴학증명서 등을 일일이 확인하는 작업이 너무 번거롭고 힘들었습니다.

그렇지만 저는 온사이트 대회를 준비했던 건 아니었기 때문에 다른 해보다는 비교적 쉽게 준비한 것이 아닌가 싶습니다.
놓쳤던 것들
대회 중에 발생한 이런저런 예외적인 상황들에 대해 제대로 and/or 빠르게 대처하지 못했던 게 아쉬웠습니다. 앞서 언급했던 것들만 다시 언급하자면, 가령…
- GMail은 하루 발신 제한량이 있었고, 제가 shiftpsh.com과 ucpc.me 도메인으로 발신하기 위해 개인적으로 월정액을 내고 사용했던 메일서버에도 마찬가지로 하루 발신 제한량이 있었습니다.
- 사소하게는 call for tasks 메일 계정과 Slack을 연동시켜 주는 Zapier 스크립트가 간헐적으로 동작하지 않는 문제가 있어서 공모받은 문제를 확인하지 못할 뻔 하기도 했습니다.
- 이메일 주소를 이메일 확인 등의 방법으로 검증하지 않아 메일 전송 과정 중에서도 누락되는 메일들이 발생했습니다. Google Forms를 사용하는 대신 직접 대회 등록 사이트를 만들었다면 좋았을 것입니다. 위의 이유와 맞물려 메일을 자동으로 발송해 주는 시스템이 있었다면 더 좋았을 것입니다.
- 대회 서버가 다운되었을 때 의논할 시간이 부족한 상황에서 대회 진행 형식을 결정해야 했습니다. 이런 상황이 발생했을 때는 미리 어떻게 하면 좋겠다는 계획을 세웠더라면 참가자들의 피해와 스트레스를 줄일 수 있었을 것입니다.
- 방송 계획과 대본을 미리 짜놓지 못해 다소 매끄럽지 못하게 진행된 것 같아 아쉬웠습니다.
- (이건 예외적인 상황은 아니었고, 제가 정신없어서였지만) 제 불찰로 후원사와의 소통이 제대로 진행되지 못한 부분이 있었고, 안타깝게도 이로 인해 다소 불미스러운 일이 발생했습니다.
UCPC는 이제 예선 기준으로 참가 인원 1,000명을 바라보고 있을 정도로 커진 대회입니다. 코딩 테스트 열풍으로 인해 알고리즘 문제해결 및 경쟁 프로그래밍 입문자들이 갈수록 많아지고 있고, 이런 기조가 사그라들지 않는 한 대회 규모는 계속 커질 것으로 생각됩니다. 이런 규모의 대회라면, 이런 규모의 대회에서 일어날 수 있는 갖가지 상황들을 미리 파악하고 숙고하여 대비하는 것이 옳겠다고 뒤늦게 느낍니다.
그럼에도 좋았던 것들
우여곡절도 많았지만 전대프연으로써는 처음 시도했던 온라인 대회를 성공적으로 마무리할 수 있어서 뿌듯합니다. 코로나 시국도 프로그래밍 대회는 이기지 못했네요. 😎
대단하고 멋진 분들과 함께 최고의 커뮤니티 대회를 만들 수 있어서 즐겁고 뿌듯했습니다. 온라인 대회여서 안타깝게도 참가자 분들과는 만나지 못했지만요.
그래서 회장 1년 더 하나요?

사실 UCPC 2020 직후에도 SUAPC에서 운영과 출제를 했고, 신촌 캠프 대회와 SNUPC에서도 검수 및 조판으로 참여했습니다. UCPC에서 얻은 경험과 리소스가 상당히 많은 도움이 되었습니다.

하지만 내년에도 회장을 할지는 잘 모르겠습니다. 일단 이제 직장에 다니고 있기도 하고, 무엇보다 결정적으로 휴학생 팀으로 나간 ICPC 2020 인터넷 예선에서 너무 처참한 성적을 받았기 때문입니다.
여러 대회를 운영하고 출제하고 검수하느라 바빴고, 게다가 solved.ac 개발로도 바빴던 나머지 제가 문제해결 연습을 할 시간이 부족해져서라고 생각했고, 지금은 다시 팀 연습도 하고 코드포스도 자주 나가고 BOJ 문제도 열심히 풀고 있습니다. 내년 대회에는 참가자로서 참여하고 싶습니다. 복학할 때 적의환향赤衣還鄕해서 레드시프트 이름값 해야죠.

결론은 내년 전대프연을 이끌어 주실 분을 모십니다. 뭐 없으면 어쩔 수 없고…
마치면서
전대프연과 UCPC에 특별한 관심을 갖고 지원해 주신 고려대학교 SW중심사업단, 마인즈랩과 네이버 D2, 그리고 알고스팟의 구종만님과 케니소프트의 박현민525hm님께 깊은 감사를 드립니다. 특히 예선 서버 문제로 새벽 코딩을 불사하며 끝까지 이슈 해결을 위해 수고해 주신, 전대프연의 초대 회장이자 이제는 스타트링크의 최백준baekjoon님께 각별한 감사를 드립니다.
검수는 물론 대회 운영 전반에 있어서 기술적으로 많은 도움을 주신 박수찬tncks0121님, 훌륭한 문제를 출제해 주신 김동현kdh9949님, 김창동sait2000님, 나정휘jhnah917님, 노영훈Diuven님, 모현ahgus89님, 문창현ckdgus2482님, 반딧불79brue님, 배근우functionx님, 심유근cozyyg님, 이동관windflower님, 이상헌evenharder님, 이종영moonrabbit2님, 정기웅QuqqU님, 조창민Ronaldo님, 그리고 열정적으로 검수해 주신 류호석rhs0266님과 홍은기pichulia님께 진심으로 감사의 말씀을 드립니다.
이외에도 대회 막바지에 운영에 큰 도움을 주신 공인호inh212님, 김영현kipa00님과, 실험적인 형태의 대회임에도 대회 진행자를 흔쾌히 맡아 주신 정재헌Gravekper님께도 대단히 감사드립니다.
마지막으로, UCPC 2020에 참가해 주신, 알고리즘 문제해결을 사랑해 주시는 참가자 여러분께 감사드립니다.
대회 리소스
다른 프로그래밍 대회를 개최하시는 데 도움이 될 수 있도록 UCPC 2020에서 사용된 자료들을 인터넷에 공개했습니다.
오픈소스
- ucpcc/ucpc2020-site UCPC 2020 대회 사이트
Jekyll로 제작한 정적 사이트입니다. 대회 공지사항 등을 적기 위해 만들었습니다. - ucpcc/problemsetting-guidelines UCPC 디스크립션 작성 및 포매팅 컨벤션
UCPC 문제 제작을 위해 수립한 컨벤션입니다. 일관적인 데이터와 디스크립션 작성에 도움을 줄 수 있습니다. - ucpcc/ucpc2020-description-layout UCPC 2020 문제지 레이아웃
마개조된 olymp.sty입니다. 2019 서강대학교 프로그래밍 대회 문제지 레이아웃을 바탕으로 제작했습니다. - ucpcc/ucpc2020-solutions-theme UCPC 2020 솔루션 Beamer 테마
Beamer와 함께 사용할 수 있는 테마입니다. - ucpcc/ucpc2020-broadcast-scene UCPC 2020 방송 씬
OBS가 씬에 웹 브라우저를 사용할 수 있다는 사실에 착안하여 React로 제작한 16:9 방송 씬입니다.
공유 문서
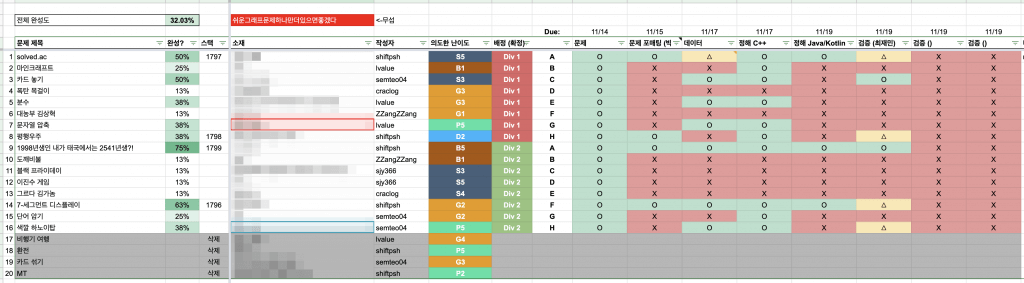
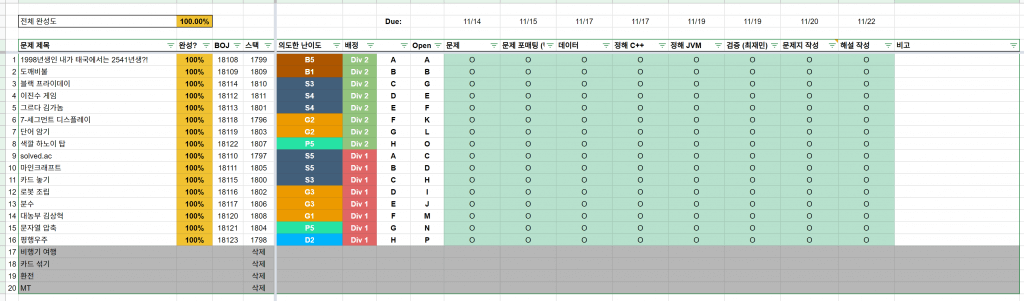
- UCPC 2020 문제 출제 현황 시트
대회 운영에 활용했던 출제 현황 시트 레이아웃입니다. 운영 당시 그대로의 시트는 아니고, 이해를 돕기 위해 체크박스 상황은 연출했으며 미사용 문제들은 다른 곳에서 사용될 수 있으므로 관련 정보를 지웠습니다. 사용하고자 하실 경우 파일 > 사본 만들기를 누르면 수정 가능한 사본을 만들어 사용해 주세요.
다른 글
- UCPC 2020 방송 후기 – 정재헌Gravekper님의 글
- UCPC 2020 출제 후기 – 이상헌evenharder님의 글
- UCPC 2020 출제 후기 – 나정휘jhnah917님의 글
- 2020년 7월 25일 서버 사고 – 최백준baekjoon님의 글
- UCPC 2019 후기 : 알고리즘 대회를 운영하기 위해서 – 안수빈subinium님의 글