
올해는 예년보다 문제들이 쉬워진 느낌이었습니다. 다섯 문제를 전부 풀었습니다.
제 풀이를 공유합니다.
1차 1번 – 친구들
사람이 $N \leq 100\,000$명 있습니다.
번호 $i$인 사람은 수 $D_i$를 갖고 있는데, $i + D_i \leq N$라면 $i$번 사람과 $i + D_i$번 사람은 친구입니다. 또, 친구의 친구는 친구입니다.
이 때, ‘극대 그룹’의 수를 찾아야 합니다.
친구 관계를 그래프로 생각해 봅시다. ‘친구의 친구가 친구‘라는 말을 잘 생각해 보면, 어떤 연결 요소 안의 모든 사람들은 서로 친구가 됩니다.
따라서 DFS/BFS 여러 번을 통해 연결 요소의 수를 세 주면 문제의 답이 됩니다. 또는 DSUdisjoint set union를 사용해도 됩니다. DFS/BFS를 사용하면 $\mathcal{O}\left(N\right)$만에 해결할 수 있습니다.
저는 DSU를 사용해서 풀었습니다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using pii = pair<int, int>;
/* [t] [c] [s] */
int dsu[100001];
int find(int u) {
return dsu[u] == u ? u : (dsu[u] = find(dsu[u]));
}
void merge(int u, int v) {
u = find(u), v = find(v);
if (u != v) dsu[v] = u;
}
void solve() {
int n;
cin >> n;
iota(dsu + 1, dsu + 1 + n, 1);
for (int i = 1; i <= n; i++) {
int x;
cin >> x;
if (i + x > n) continue;
merge(i, i + x);
}
set<int> s;
for (int i = 1; i <= n; i++) s.emplace(find(i));
cout << s.size() << endl;
}
int main() {
cin.tie(nullptr), cout.tie(nullptr), ios::sync_with_stdio(false);
#ifdef _SHIFTPSH
freopen("_run/in.txt", "r", stdin), freopen("_run/out.txt", "w", stdout);
#endif
int t;
cin >> t;
for (int _ = 1; _ <= t; _++) {
cout << "Case #" << _ << endl;
solve();
}
return 0;
}
DSU를 만들 때 std::iota라는 좋은 함수를 사용하면 쉽고 빠르게 초기화할 수 있습니다. STL에 이런 함수가 있다는 게 좀 의외일까요?
1차 2번 – 이진수
길이가 $n \leq 50\,000$인 비트 문자열 $a$가 있고, 같은 길이의 비트 문자열 $b$를 다음과 같이 정의합니다. $\vee$는 OR 연산입니다.
\[b_i = \left(a_{i-t} \vee a_{i+t}\right)\]
$b$가 주어지면, 사전순으로 제일 앞서는 $a$를 구해야 합니다.
약간 헤멜 수 있는 문제였던 것 같습니다. 일단 두 가지 사실을 기반으로 생각해봅시다.
- $b_i$가 켜져 있다면, $a_{i-t}$ 또는 $a_{i+t}$가 켜져 있어야 합니다.
- $a_i$가 켜져 있다면, $b_{i-t}$와 $b_{i+t}$가 모두 켜져 있어야 합니다.
이제 $b_i$를 왼쪽부터 보면서, 켜져 있으면서 아직 $a_{i-t}$와 $a_{i+t}$ 모두가 꺼져 있는 $b_i$들에 대해, 그리디하게 $a$의 비트들을 켜 줍니다.
- 오른쪽($a_{i+t}$) 비트를 켤 수 있으면 켜 줍니다. 오른쪽 비트를 켤 수 있으려면, $b_{i+2t}$가 존재하지 않거나 켜져 있어야 합니다. 이는 사전 순으로 가장 먼저 오는 $a$를 구성하기 위함입니다.
- 오른쪽 비트를 켤 수 없다면 왼쪽($a_{i-t}$) 비트를 켜 줍니다.
생각해 보면 모든 $b_i$에 대해 둘 중 하나 이상을 켤 수 있는 경우만 입력으로 주어진다는 사실을 알 수 있습니다. 이를 그대로 구현해 주면 됩니다. $\mathcal{O}\left(n\right)$만에 해결할 수 있습니다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using pii = pair<int, int>;
/* [t] [c] [s] */
void solve() {
int n, t;
cin >> n >> t;
string b;
cin >> b;
vector<int> a(n);
for (int i = 0; i < n; i++) {
if (b[i] == '0') continue;
int l = i - t, r = i + t;
if ((l >= 0 && a[l]) || (r < n && a[r])) continue;
int ll = l - t, rr = r + t;
if (r < n) {
if (rr >= n || b[rr] == '1') {
a[r] = 1;
continue;
}
}
if (l >= 0) {
if (ll < 0 || b[ll] == '1') {
a[l] = 1;
continue;
}
}
}
for (int i = 0; i < n; i++) cout << a[i];
cout << endl;
}
int main() {
cin.tie(nullptr), cout.tie(nullptr), ios::sync_with_stdio(false);
#ifdef _SHIFTPSH
freopen("_run/in.txt", "r", stdin), freopen("_run/out.txt", "w", stdout);
#endif
int t;
cin >> t;
for (int _ = 1; _ <= t; _++) {
cout << "Case #" << _ << endl;
solve();
}
return 0;
}
1차 3번 – No Cycle
정점 $N \leq 500$개, 간선 $M+K$개의 그래프가 있습니다. $M+K$의 간선 중 $M \leq 2\,000$개는 방향이 있고, $K \leq 2\,000$개는 방향이 정해지지 않았습니다.
이 때 $K$개의 간선들의 방향을 잘 정해서, 사이클이 없는 그래프를 구성하고 싶습니다. 방향이 정해진 $M$개의 간선들만 있는 경우에는 사이클이 없는 상태입니다.
답은 $K$글자의 비트 문자열입니다. 방향이 없는 $i$번째 간선의 입력이 $\textcolor{#ff3b57}{u}$ $\textcolor{#ffb717}{v}$로 주어졌을 때, $\textcolor{#ff3b57}{u} \rightarrow\textcolor{#ffb717}{v}$로 방향을 정했다면 $0$, $\textcolor{#ffb717}{v} \rightarrow \textcolor{#ff3b57}{u}$로 방향을 정했다면 $1$입니다. 이 때 사전 순으로 가장 앞서는 비트 문자열을 출력해야 합니다.
사이클이 없는 방향 그래프에서, 임의의 정점 $\textcolor{#ff3b57}{u}$와 $\textcolor{#ffb717}{v}$를 고르고 그 정점을 잇는 간선을 추가한다고 생각해 봅시다. $\textcolor{#ff3b57}{u} \rightarrow\textcolor{#ffb717}{v}$로 정할 수도 있고 $\textcolor{#ffb717}{v} \rightarrow \textcolor{#ff3b57}{u}$로 정할 수도 있습니다. 두 경우 모두가 사이클을 만드는 경우가 있을까요?
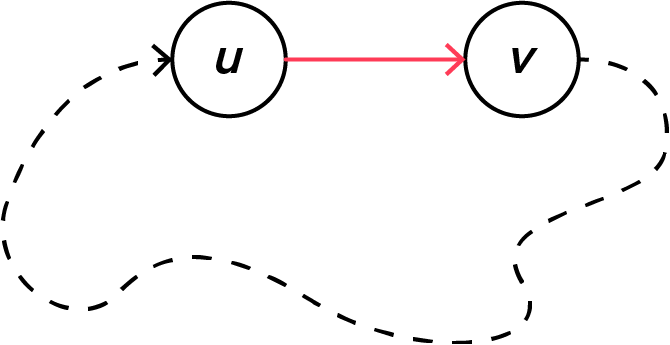
$\textcolor{#ff3b57}{u} \rightarrow\textcolor{#ffb717}{v}$라는 간선을 추가했을 때 사이클이 생긴다는 것은, $\textcolor{#ffb717}{v} \rightarrow \textcolor{#ff3b57}{u}$로 가는 경로가 이미 존재한다는 사실과 동치입니다.
따라서 $\textcolor{#ff3b57}{u} \rightarrow\textcolor{#ffb717}{v}$도 사이클을 만들고 $\textcolor{#ffb717}{v} \rightarrow \textcolor{#ff3b57}{u}$도 사이클을 만든다면, 각각 $\textcolor{#ffb717}{v} \rightarrow \textcolor{#ff3b57}{u}$라는 경로와 $\textcolor{#ff3b57}{u} \rightarrow\textcolor{#ffb717}{v}$라는 경로 모두가 이미 존재해야 됩니다.
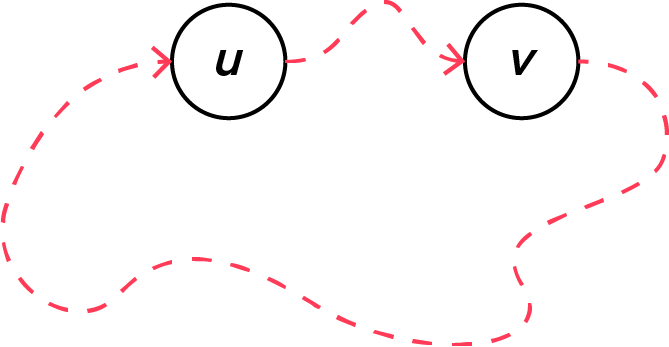
하지만 그런 두 개의 경로가 이미 존재한다면, 그 두 개의 경로만으로 사이클을 만들 수 있습니다. 이는 우리가 처음에 한 가정 — 사이클이 없는 방향 그래프 — 에 모순됩니다. 따라서 $\textcolor{#ff3b57}{u} \rightarrow\textcolor{#ffb717}{v}$와 $\textcolor{#ffb717}{v} \rightarrow \textcolor{#ff3b57}{u}$ 중 적어도 하나는 새로운 사이클을 만들지 않는다는 사실을 알 수 있습니다.
그러므로 이미 사이클이 없는 방향 그래프라면, 간선들을 무한정 추가해줄 수 있습니다. 그래프의 정점과 간선의 수가 작기 때문에, 간선을 추가해줄 때마다 사이클이 생기는지 생기지 않는지 확인하면서 간선을 하나씩 추가해나갈 수 있습니다.
사전 순으로 가장 앞서는 비트 문자열을 구성해야 하므로, 우선 $\textcolor{#ff3b57}{u} \rightarrow\textcolor{#ffb717}{v}$를 추가한 뒤 사이클이 안 생긴다면 그대로 가져갑니다. 사이클이 생긴다면 위의 증명을 통해 $\textcolor{#ffb717}{v} \rightarrow \textcolor{#ff3b57}{u}$를 추가해줄 수 있음이 보장된다는 것을 알 수 있으므로, 그렇게 해 줍니다.
사이클의 존재 여부를 판단하는 방법은 여러 가지가 있습니다. 저는 DFS로 구현했습니다. 그래프가 연결 그래프임은 보장되지 않으므로, 방문하지 않은 모든 정점에서 DFS를 시작해야 함에 유의합니다.
간선을 $K$개 추가해 주고, 추가할 때마다 DFS를 한 번 해야 하므로 $\mathcal{O}\left(K\left(N+K+M\right)\right)$의 시간이 걸립니다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using pii = pair<int, int>;
/* [t] [c] [s] */
bitset<501> root;
int vis[501], ans[2000];
bool dfs(int u, const vector<vector<int>> &graph) {
// check for cycles
if (vis[u]) return vis[u] == -1;
vis[u] = -1;
for (int v : graph[u]) {
if (dfs(v, graph)) return true;
}
vis[u] = 1;
return false;
}
void solve() {
int n, m, k;
cin >> n >> m >> k;
root.reset(), root.flip();
vector<vector<int>> graph(n + 1);
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
graph[u].emplace_back(v);
}
for (int i = 0; i < k; i++) {
int u, v;
cin >> u >> v;
// 0?
graph[u].emplace_back(v);
memset(vis, 0, sizeof vis);
bool flag = true;
for (int x = 1; x <= n; x++) {
if (vis[x]) continue;
if (dfs(x, graph)) {
flag = false;
break;
}
}
ans[i] = !flag;
if (flag) continue;
// 1?
graph[u].pop_back();
graph[v].emplace_back(u);
}
for (int i = 0; i < k; i++) cout << ans[i];
cout << endl;
}
int main() {
cin.tie(nullptr), cout.tie(nullptr), ios::sync_with_stdio(false);
#ifdef _SHIFTPSH
freopen("_run/in.txt", "r", stdin), freopen("_run/out.txt", "w", stdout);
#endif
int t;
cin >> t;
for (int _ = 1; _ <= t; _++) {
cout << "Case #" << _ << endl;
solve();
}
return 0;
}
1차 4번 – 예약 시스템
$2 \times m$개의 방이 있는 호텔이 있습니다. $m \leq 50\,000$입니다.
$n\leq 20\,000$개 그룹의 투숙객들이 호텔에 묵으려 합니다. 각 그룹의 크기는 $5$ 이상이고, 한 명이 한 개의 방에 묵습니다.
모든 투숙객들은 스트레스 지수 $w_i$를 갖고 있어서, 인접한 방에 다른 그룹의 투숙객이 있고 그 투숙객의 스트레스 지수가 $w_j$라면, 그 쌍에 대해 $w_i + w_j$만큼의 충돌이 발생합니다. 모든 쌍에 대해 충돌의 합을 최소화하고 싶습니다.
(그냥 이렇게 설명하면 끝나는 문제인데, SCPC 운영진은 디스크립션을 어렵게 쓰는 재주가 있는 걸까요?)
SCPC의 서브태스크는 보통은 만점 풀이와는 무관한 브루트포스 풀이를 요구하는 경향이 있는데, 이 문제는 서브태스크 순서대로 생각해 보면 정해 풀이까지 다다를 수 있는 문제였다고 생각합니다.
문제를 처음 읽으면 어떻게 배치해야 될지 조차 감이 오지 않지만 서브태스크가 그룹 크기가 홀수 또는 짝수인 경우로 나뉘어 있다는 점에서 착안해 아래와 같은 접근을 시작할 수 있었습니다.
서브태스크 1: 그룹이 모두 짝수인 경우
우선 그룹의 크기 $l_i$가 모두 짝수일 때의 경우, 최적의 배치가 어떻게 되는지 생각해 봅시다. 다른 그룹과 ‘닿는’ 부분이 최소화되면 좋을 것 같습니다. 그런 배치는 아래 그림과 같이, $2 \times \frac{l_i}{2}$ 직사각형들을 이어 붙인 경우가 됩니다.
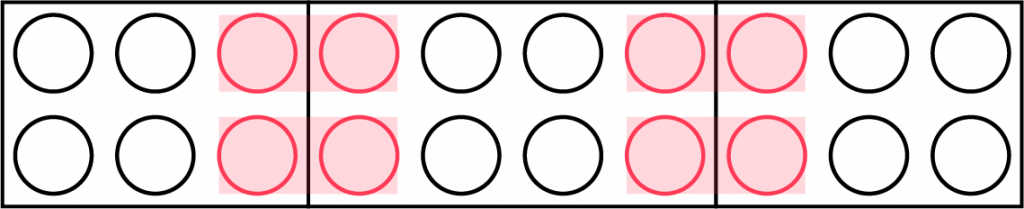
이 때 핑크색으로 칠한 부분에서 충돌이 일어납니다.
그룹의 순서가 정해져 있을 때 충돌의 합을 최소화하려면, 첫 번째 그룹과 마지막 그룹에서는 제일 작은 원소 $2$개씩을 고르고, 나머지 그룹에서는 제일 작은 원소 $4$개씩을 고르면 됩니다.
다르게 생각한다면 모든 그룹에서 제일 작은 원소 $4$개씩을 고른 후, 두 개의 그룹에서만 $3$번째로 작은 원소와 $4$번째로 작은 원소 하나씩을 빼 주면 됩니다.
$i$번째 그룹에서 $j$번째로 작은 원소를 $m_{i,j}$라고 합시다. 그러면 모든 그룹을 $m_{i,3}+m_{i,4}$ 순으로 정렬한 후, $\sum_i \left(m_{i,1}+m_{i,2}+m_{i,3}+m_{i+4}\right)$에서 $m_{i,3}+m_{i,4}$가 제일 큰 두 그룹만 빼 주면 정답입니다.
서브태스크 2: 그룹이 모두 홀수인 경우
짝수인 경우와 비슷하게 배치해줄 수 있습니다.

이 경우에는 충돌이 조금 더 많이 생기긴 합니다만, 짝수의 경우와 비슷하게 접근할 수 있습니다.
우선 각 그룹마다 두 번씩 충돌이 일어나는 원소가 하나 있는데, 이를 그 그룹에서 가장 작은 원소로 둡시다. 그러면 모든 그룹에서 제일 작은 원소 $4$개씩을 고른 후, 두 개의 그룹에서만 $3$번째로 작은 원소와 $4$번째로 작은 원소 하나씩을 빼 주면 되는 것은 동일합니다만, 가장 작은 원소는 한 번 더 더해줘야 합니다.
다시 말하면 모든 그룹을 $m_{i,3}+m_{i,4}$ 순으로 정렬한 후, $\sum_i \left(\textcolor{#ff3b57}{2m_{i,1}}+m_{i,2}+m_{i,3}+m_{i+4}\right)$에서 $m_{i,3}+m_{i,4}$가 제일 큰 두 그룹만 빼 주면 정답입니다.
서브태스크 3: 짝수 그룹과 홀수 그룹이 섞여 있는 경우
위에서의 접근을 바탕으로, 크게는 $3$가지 경우로 나눠 생각할 수 있습니다.
- 짝수 그룹과 홀수 그룹이 하나 이상씩 있다면, 맨 왼쪽 그룹과 맨 오른쪽 그룹에 짝수 그룹 하나와 홀수 그룹 하나씩이 있는 경우
- 짝수 그룹의 개수가 $2$개 이상이라면, 맨 왼쪽 그룹과 맨 오른쪽 그룹이 모두 짝수 그룹인 경우
- 홀수 그룹의 개수가 $2$개 이상이라면, 맨 왼쪽 그룹과 맨 오른쪽 그룹이 모두 홀수 그룹인 경우
3a: 맨 왼쪽 그룹과 맨 오른쪽 그룹에 짝수 그룹 하나와 홀수 그룹 하나씩이 있는 경우

먼저 홀수 그룹들을 전부 왼쪽에 배치하고, 나머지 짝수 그룹들을 전부 오른쪽에 배치합시다.
짝수 그룹 중 $m_{i,3}+m_{i,4}$가 가장 큰 그룹 하나와, 홀수 그룹 중 $m_{i,3}+m_{i,4}$가 가장 큰 그룹 하나를 골라서 빼 주면 됩니다.
3b: 맨 왼쪽 그룹과 맨 오른쪽 그룹이 모두 짝수 그룹인 경우
위의 경우와 비슷합니다. 오른쪽에 있는 짝수 그룹들 중 하나를 빼다가 맨 왼쪽에 붙이면 됩니다.
짝수 그룹 중 $m_{i,3}+m_{i,4}$가 가장 큰 그룹 두 개를 골라서 빼 주면 됩니다.
3c: 맨 왼쪽 그룹과 맨 오른쪽 그룹이 모두 홀수 그룹인 경우
이 경우는 약간 까다롭습니다.
일단 홀수 그룹 두 개를 잘 합치면 직사각형을 만들 수 있다는 점에서 착안해 아래와 같은 배치를 생각할 수 있습니다.

이 경우, 홀수 그룹 중 $m_{i,3}+m_{i,4}$가 가장 큰 그룹 두 개를 골라서 빼 주면 됩니다.
하지만 이런 경우는 홀수 그룹이 $4$개 이상인 경우에만 만들 수 있습니다. 홀수 그룹이 $2$개라면 어쩔 수 없이 아래와 같은 경우로 구성해야 합니다.

이 경우에는, 짝수 그룹들에서 $\sum_i \left(\textcolor{#ff3b57}{2m_{i,1}}+\textcolor{#ff3b57}{2m_{i,2}}+m_{i,3}+m_{i+4}\right)$를 해 줘야 합니다. 홀수 그룹이 $2$개인 경우에만 특수하게 처리해줍시다.
모든 경우를 고려한 코드는 아래와 같습니다. 정렬이 필요하기 때문에 $\mathcal{O}\left(n \log n\right)$만큼의 시간이 걸립니다. 사실 제일 큰 두 개 그룹만 구해도 상관없기 때문에, 잘 짠다면 $\mathcal{O}\left(n\right)$도 가능하지만요.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using pii = pair<int, int>;
/* [t] [c] [s] */
int a[100000];
pii p[20000];
void solve() {
int n, m;
cin >> n >> m;
ll s = 0, sa = 0;
ll oc = 0, ec = 0;
for (int i = 0; i < n; i++) {
int l;
cin >> l;
for (int j = 0; j < l; j++) cin >> a[j];
sort(a, a + l);
((l & 1) ? oc : ec)++;
p[i].first = a[2] + a[3];
p[i].second = (l & 1);
s += (1 + (l & 1)) * a[0] + a[1] + a[2] + a[3];
sa += 2 * a[0] + (2 - (l & 1)) * a[1] + a[2] + a[3];
}
sort(p, p + n, greater<>());
if (oc && ec) {
ll coe = 0, coo = 0, cee = 0;
// coe: o o .. o e .. e e
int o = 0, e = 0;
for (int i = 0; i < n; i++) {
if (!o && p[i].second) {
coe += p[i].first;
o++;
}
if (!e && !p[i].second) {
coe += p[i].first;
e++;
}
if (o && e) break;
}
// coo: o o .. o e .. e o .. o o
if (oc >= 2) {
o = 0;
for (int i = 0; i < n; i++) {
if (o < 2 && p[i].second) {
coo += p[i].first;
o++;
}
if (o >= 2) break;
}
}
// cee: e e .. e o .. o e .. e e
if (ec >= 2) {
e = 0;
for (int i = 0; i < n; i++) {
if (e < 2 && !p[i].second) {
cee += p[i].first;
e++;
}
if (e >= 2) break;
}
}
vector<ll> cd;
cd.emplace_back(s - coe);
cd.emplace_back(sa - coo);
cd.emplace_back(s - cee);
if (oc >= 4) cd.emplace_back(s - coo);
s = *min_element(cd.begin(), cd.end());
} else {
s -= p[0].first + p[1].first;
}
cout << s << endl;
}
int main() {
cin.tie(nullptr), cout.tie(nullptr), ios::sync_with_stdio(false);
#ifdef _SHIFTPSH
freopen("_run/in.txt", "r", stdin), freopen("_run/out.txt", "w", stdout);
#endif
int t;
cin >> t;
for (int _ = 1; _ <= t; _++) {
cout << "Case #" << _ << endl;
solve();
}
return 0;
}
$s$는 다음의 합입니다.
\[s=\sum_i \begin{cases}m_{i,1}+m_{i,2}+m_{i,3}+m_{i,4} &\text{if } l_i\text{ is even}\\ 2m_{i,1}+m_{i,2}+m_{i,3}+m_{i,4} &\text{if } l_i\text{ is odd}\end{cases}\]
$sa$는 홀수 그룹이 $2$개인 경우 특수 처리를 해 주기 위한 값으로서 다음의 합입니다.
\[sa=\sum_i \begin{cases}2m_{i,1}+2m_{i,2}+m_{i,3}+m_{i,4} &\text{if } l_i\text{ is even}\\ 2m_{i,1}+m_{i,2}+m_{i,3}+m_{i,4} &\text{if } l_i\text{ is odd}\end{cases}\]
배열 $p$에는 모든 그룹들에 대해 홀/짝 정보와 $m_{i,3}+m_{i,4}$ 정보를 저장해 두고 정렬했습니다.
여담

이 문제는 오후 7시 33분에 한 번 수정되었습니다.
예약 시스템 문제에서 조건이 하나 빠져 있었습니다. 아래와 같이 명시했고, 제출 횟수를 20회로 늘릴 것입니다.
– 한 집합에 속한 예약자들은 모두 한 덩어리의 방들을 배정 받아야 한다. 한 덩어리의 방들이란 덩어리에 속한 어떤 방 두개에 대해서도, 덩어리에 속하고 인접한 방들을 통해서 이동이 가능하다는 의미이다.
그런 말이 쓰여 있지는 않았지만, 운이 좋게도? 당연히 연결 요소여야 최소일 것이라고 생각하고 풀었고, 문제를 맞을 수 있었습니다. 연결 요소가 아니어도 괜찮았을 경우, 다음과 같은 반례가 있습니다.
1 5 14 6 1 1 1 1 1 1 6 2 2 2 2 2 2 6 2 2 2 2 2 2 5 10 10 10 10 10 5 10 10 10 10 10
이 경우 아래와 같은 구성이 가능합니다.
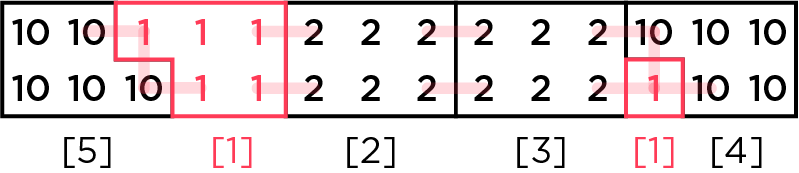
이 때 답은 $84$입니다.
1차 5번 – 차이
$100\,000$개 이하의 미지수 $X_i$들에 대해 다음 쿼리들을 수행해야 합니다. 쿼리의 수는 $200\,000$개 이하입니다.
1 i j d: $X_i + d = X_j$라는 조건을 추가합니다.2 i j: $X_i-X_j$를 출력합니다. 조건이 모순된다면CF를, 주어진 조건들만으로 알 수 없다면NC를 출력합니다.
$d$가 없다면 간단한 DSU 문제입니다. 이걸로 서브태스크 1과 3을 쉽게 해결할 수 있습니다.
DSU 트리의 간선들에 가중치가 있다고 생각한다면 서브태스크 2와 4를 해결할 수 있습니다.
우리가 DSU 쿼리를 $\mathcal{O}\left(\alpha\left(N\right)\right)$만에 할 수 있는 이유는 경로 압축path compression이라는 좋은 테크닉이 있어서입니다. $p_u$가 노드 $u$의 부모 노드라고 한다면, $u$의 루트를 구하는 함수 $\mathrm{find}$에서 경로 압축은 다음과 같이 재귀적으로 수행했습니다.
\[\mathrm{find}\left(u\right) = \begin{cases} u & \text{if } u=p_u \\ p_u \leftarrow \mathrm{find}\left(p_u\right) & \text{otherwise} \end{cases}\]
이렇게 하면 $u$에서 $u$의 루트 $r$로 가는 경로 위에 있는 모든 정점들의 부모가 아예 $r$로 바뀌어 버리게 됩니다.
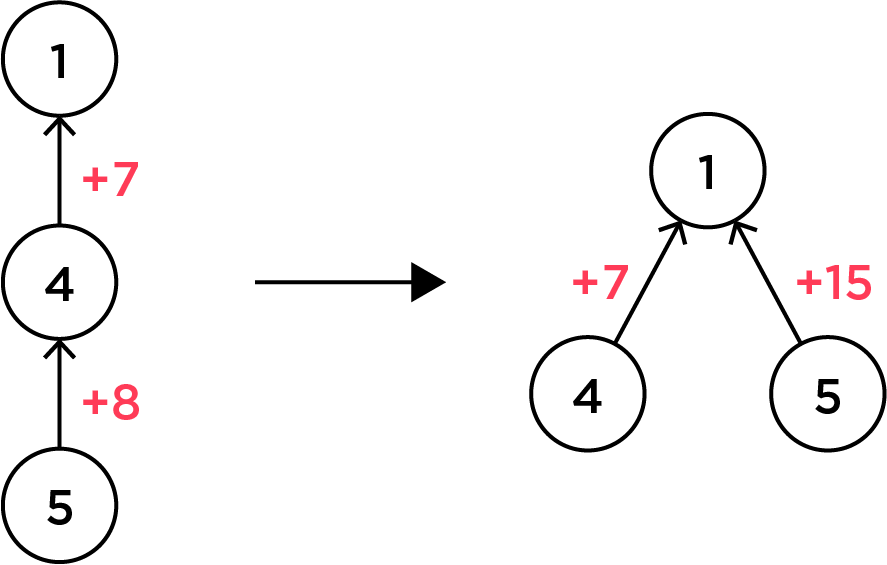
현재 노드 $u$에서 부모 노드 $p_u$로 가는 비용을 $d_u$라고 합시다. 그러면 $d_u$도 비슷한 방법으로 압축해버릴 수 있습니다.
$\mathrm{find}$ 함수를 돌릴 때 $u$의 부모 노드는 $p_u$였고, $p_u$의 부모 노드는 $r$이었습니다. 따라서 $u$에서 $r$까지 가는 데는 $d_u + d_{p_u}$만큼의 비용이 필요합니다. $\mathrm{find}$ 함수에서 경로 압축을 수행하면서, $d_u$를 $d_u + d_{p_u}$로 업데이트해 주면 됩니다. 이제 가중치가 있는 DSU 트리에서도 경로 압축을 할 수 있습니다.
1번 쿼리와 2번 쿼리 모두 $\mathcal{O}\left(\alpha\left(N\right)\right)$만큼의 시간이 걸립니다. 총 시간 복잡도는 $\mathcal{O}\left(K\alpha\left(N\right)\right)$입니다.
$\alpha$는 역 아커만 함수inverse Ackermann function이며, $\alpha\left(2^{2^{2^{65536}}}-3\right)=4$ 정도로 작기 때문에 상수라고 생각해도 무방합니다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using pii = pair<int, int>;
/* [t] [c] [s] */
int dsu[100001], conf[100001];
ll val[100001]; // [u] + val[u] = [dsu[u]]
int find(int u) {
if (dsu[u] == u) return u;
int pp = find(dsu[u]);
val[u] += val[dsu[u]], dsu[u] = pp;
return pp;
}
bool merge(int u, int v, ll x) {
// [u] + x = [v]
if (find(u) == find(v)) {
if (val[u] + x != val[v]) {
conf[find(u)] = true;
return false;
}
return true;
}
int pu = find(u);
x += val[u];
int pv = find(v);
x -= val[v];
u = pu, v = pv;
val[u] = val[v] - x, dsu[u] = v;
conf[v] |= conf[u];
return true;
}
void solve() {
int n, q;
cin >> n >> q;
iota(dsu + 1, dsu + n + 1, 1);
memset(conf, 0, sizeof conf);
memset(val, 0, sizeof val);
while (q--) {
int op;
cin >> op;
if (op == 1) {
int i, j, d;
cin >> i >> j >> d;
merge(i, j, -d);
} else {
int i, j;
cin >> i >> j;
int pi = find(i), pj = find(j);
if (pi != pj) {
cout << "NC\n";
} else if (conf[pi]) {
cout << "CF\n";
} else {
cout << val[i] - val[j] << '\n';
}
}
}
cout.flush();
}
int main() {
cin.tie(nullptr), cout.tie(nullptr), ios::sync_with_stdio(false);
#ifdef _SHIFTPSH
freopen("_run/in.txt", "r", stdin), freopen("_run/out.txt", "w", stdout);
#endif
int t;
cin >> t;
for (int _ = 1; _ <= t; _++) {
cout << "Case #" << _ << endl;
solve();
}
return 0;
}
conf는 모순이 발생했는지 여부를 저장하는 배열입니다. find 함수가 항상 루트를 찾아주기 때문에, conf 플래그도 맨 위에만 달면 충분합니다.
긴 시간 문제 푸시느라 모두 수고하셨습니다. 라운드 2에서 만납시다!
시프트님 팬이에요
안녕하세요 알고리즘 막 입문한 학생입니다 🙂
아직 그래프이론을 잘 이해하지 못하여서, 이번 SCPC 1번 문제에서 제 알고리즘이 혹여 DFS나 DSU와 결과적으로 똑같은 것인지 질문 드립니다.
모든 사람이 들고있는 수가 자연수임에 착안하여 1번부터 출발점을 잡고, 1번 사람에게 있는 자연수만큼 더한 수의 번호로 이동하게 합니다. 그와 동시에 이미 선택된 자연수는 더이상 선택되지 않도록 flag를 켜줍니다. 그렇게 계속 탐색하다가 i+arr[i]가 N을 넘어간다면 count++을 해주고, flag가 켜져있는 수를 만나면 continue;를 이용하여 1번부터 N까지 반복을 하였습니다. 이또한 시간복잡도가 N인것으로 생각되는데, 이 알고리즘이 결과적으로는 그래프 이론을 이용한 풀이와 같은 것인지 궁금해서 답글 남깁니다!
안녕하세요, 말씀해주신 방법도 유효하고, 어떻게 보면 DFS와 비슷한 방법이라고 생각할 수 있을 것 같습니다. (DSU와는 무관합니다.)
글에서 언급하진 않았지만 이 문제에서 간선은 항상 인덱스가 증가하는 방향으로 그려집니다. 그래서 그래프를 만든다면 일자 모양으로 쭉 늘어나 있는 형태가 여러 개 나올 것입니다. 그래프의 모양이 특수하기 때문에 말씀해주신 방법과 DFS/BFS는 같은 방식으로 동작하게 됩니다.
설명 감사합니다!
풀이 감사합니다!!
설명과 그림을 같이 보니 더 이해가 잘 가는것 같아요!
혹시 그림은 어떤 툴로 그리신 건가요??
그림은 Adobe Illustrator로 그리고 있습니다. 감사합니다 🙏