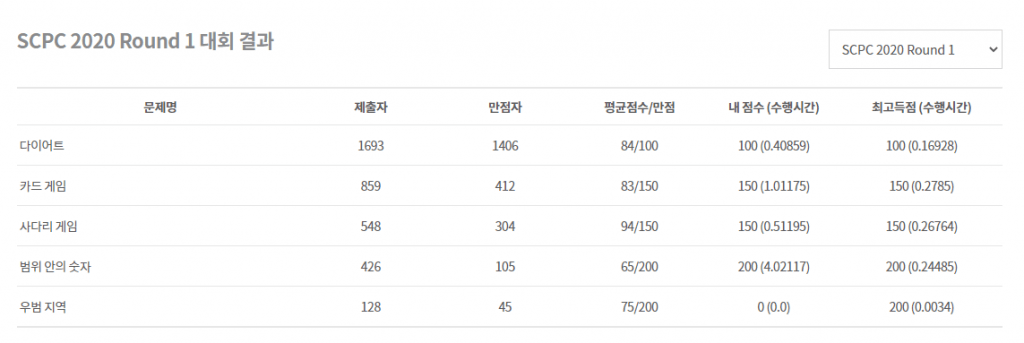
1차 예선에서 1, 2, 3, 4번을 풀어서 800점 만점에 600점을 받았습니다. 부분 점수는 안 못 받았습니다.
다음 날 수술이 있었고, 4번까지 풀고 나니 새벽이어서 5번은 안 풀고 잤습니다. 전체적으로 디스크립션이 난해한 느낌이라 안타까웠습니다.
제 1차 1, 2, 3, 4번 풀이를 공유합니다.
1차 1번 – 다이어트
A 식당과 B 식당이 있고, 이 식당에는 각각 $N \leq 50\ 000$개의 메뉴가 있습니다. 이 메뉴들의 칼로리 값들이 주어집니다. $K$일동안 매일 A에서 한 끼를, B에서 한 끼를 먹을 때, 하루에 먹은 칼로리의 양의 최댓값이 최소가 되게 하고 싶습니다.
A 식당에서의 최대 칼로리의 음식을 순서대로, B 식당에서 최소 칼로리의 음식을 순서대로 $K$일간 하나하나 그리디하게 매칭해 주면 됩니다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using uint = unsigned int;
using ull = unsigned long long;
using pii = pair<int, int>;
/* [t] [c] [s] */
int a[200000], b[200000];
int main() {
cin.tie(nullptr);
cout.tie(nullptr);
ios_base::sync_with_stdio(false);
int tt;
cin >> tt;
for (int _ = 1; _ <= tt; _++) {
cout << "Case #" << _ << "\n";
int n, k;
cin >> n >> k;
for (int i = 0; i < n; i++) cin >> a[i];
sort(a, a + n);
for (int i = 0; i < n; i++) cin >> b[i];
sort(b, b + n);
int mx = 0;
for (int i = 0; i < k; i++) mx = max(mx, a[i] + b[k - i - 1]);
cout << mx << '\n';
}
return 0;
}
1차 2번 – 카드 게임
$N \leq 3\ 000$개의 카드가 쌓여 있는 두 덱 X와 Y가 있습니다. 각 카드에는 $K \leq 3\ 000$ 이하의 양의 정수가 적혀 있습니다. 두 명이 번갈아 카드를 가져가는데,
- 꼭 한 개의 덱을 선택해서 위에서부터 한 장 이상을 가져가야 하며,
- 가져간 카드의 합이 $K$ 이하여야 하고,
- 마지막으로 카드를 가져가는 사람이 집니다.
내 턴에 덱 X에 $i$장의 카드가, 덱 Y에 $j$장의 카드가 남아 있는 상태를 $\left(i,j\right)$라고 한다면, $N$과 $K$가 정해져 있는 게임에 대해 중간 상태로 가능한 경우는 총 $\left(N+1\right)^2$개입니다. 각각의 상태에서 두 플레이어가 각각 최선의 방법으로 플레이했을 때 내가 반드시 이기는 경우와 반드시 지는 경우의 갯수를 세고 싶습니다.
Grundy number를 바로 떠올릴 수 있겠지만, 아쉽게도 마지막으로 카드를 가져가는 사람이 지는 게임(misère)이기 때문에 Grundy를 쓸 수 없습니다. Grundy로 접근하기 전에 ‘이게 1차 예선 2번에 나올 수 있을 만한 지식인가?’를 생각해 볼 필요가 있습니다.
대신 다이나믹 프로그래밍으로 접근할 수 있습니다.
- 현재 상태 $\left(i,j\right)$에서 내가 어떤 덱에서 얼마나 많이 가져가더라도 다음 플레이어가 이기는 상태만 나온다면, 현재 상태는 내가 지는 상태입니다.
- 그렇지 않다면, 내가 특정한 동작을 하면 다음 플레이어가 지는 상태를 만들 수 있습니다. 이런 경우 현재 상태는 내가 이기는 상태입니다.
따라서, DP 테이블을 만들어둔 후 가져간 카드의 합이 $K$ 이하가 되도록 X에서 하나씩, Y에서 하나씩 가져가면서 다음 플레이어가 이기는 상태가 있는지 확인해 주면 됩니다. 이 계산을 $\left(N+1\right)^2$개에 대해 하므로, $\mathcal{O}\left(N^3\right)$입니다.
$N \leq 3\ 000$이므로 Large 셋을 풀기에는 불충분합니다. 이는 Prefix sum을 이용해 $\mathcal{O}\left(N^2\right)$로 최적화할 수 있습니다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using uint = unsigned int;
using ull = unsigned long long;
using pii = pair<int, int>;
/* [t] [c] [s] */
int x[3010], y[3010], xp[3010], yp[3010], xi[3010], yj[3010];
bitset<3010> dp[3010];
int prs[3010][3010];
int main() {
cin.tie(nullptr);
cout.tie(nullptr);
ios_base::sync_with_stdio(false);
int tt;
cin >> tt;
for (int _ = 1; _ <= tt; _++) {
cout << "Case #" << _ << "\n";
memset(dp, 0, sizeof dp);
dp[0][0] = true;
int n, k;
cin >> n >> k;
for (int i = 1; i <= n; i++) {
cin >> x[i], xp[i] = x[i] + xp[i - 1];
int v = xp[i] - k - 1;
int ii = upper_bound(xp, xp + i, v) - xp;
xi[i] = ii;
}
for (int j = 1; j <= n; j++) {
cin >> y[j], yp[j] = y[j] + yp[j - 1];
int v = yp[j] - k - 1;
int jj = upper_bound(yp, yp + j, v) - yp;
yj[j] = jj;
}
int a = 0, b = 0;
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= n; j++) {
int xc = (prs[i][j + 1] - prs[xi[i]][j + 1] - prs[i][j] + prs[xi[i]][j]);
int yc = (prs[i + 1][j] - prs[i + 1][yj[j]] - prs[i][j] + prs[i][yj[j]]);
dp[i][j] = ((i - xi[i]) - xc) || ((j - yj[j]) - yc);
dp[0][0] = true;
(dp[i][j] ? a : b)++;
prs[i + 1][j + 1] = dp[i][j] + prs[i][j + 1] + prs[i + 1][j] - prs[i][j];
}
}
cout << prs[n + 1][n + 1] << ' ' << (n + 1) * (n + 1) - prs[n + 1][n + 1] << endl;
}
return 0;
}
1차 3번 – 사다리 게임
$N \leq 1\ 500$개의 세로선과 $K \leq 2\ 000$개의 가로선이 있는 사다리가 있습니다.
$M \leq 100\ 000$개의 쿼리가 들어옵니다. $\left(i,j\right)$의 형태입니다. 위의 $i$번 위치에서 시작해서 아래의 $j$번 위치에서 끝나도록 가로선을 적절히 없애 사다리를 조작하고 싶은데, 가로선을 최소한으로 없앴을 때 몇 개 없애야 하는지를 구해야 합니다.
Kotlin Heroes: Episode 4의 E번 문제와 상당히 비슷합니다.
가로선들이 그래프의 간선들이라고 생각하고 접근해서 최단 거리 문제로 해결했습니다.
$u$와 $v$를 잇는 가로선이 있다면, 가로선을 무시하는 경우($u \rightarrow u$, $v \rightarrow v$)를 가중치 $1$로, 무시하지 않는 경우($u \rightarrow v$, $v \rightarrow u$)를 가중치 $0$으로 하여 간선 $4$개로 만들어 줍니다.
정점은 $N$개를 처음에 만들어 주고, 가로선을 하나 처리할 때마다 가로선의 끝점에 각각 하나씩, 총 $2$개를 더 만들어 줍니다. 이렇게 그래프를 구성하면 노드는 총 $N+2K \leq 5\ 500$개가 됩니다.
이렇게 하면 각 시작점마다 Dijkstra 혹은 0-1 BFS를 돌리는 것으로 각 종점까지의 최단거리를 구하면, 그것이 시작점에서 종점까지 가면서 제거해야 하는 가로선의 개수의 최댓값이 됩니다. 이 방법을 이용해 쿼리 값들을 전부 전처리해둔 후, 쿼리가 들어오는 대로 전처리된 값들을 출력해 주려고 합니다.
만들어 준 그래프의 정점은 $N+2K$개, 간선은 $4K$개이므로 0-1 BFS의 경우 한 번에 $\mathcal{O}\left(N+K\right)$, Dijkstra의 경우 한 번에 $\mathcal{O}\left(K \log K\right)$입니다. 이를 모든 시작점에 대해 한 번씩 돌려주면 0-1 BFS의 경우 $\mathcal{O}\left(N^2+NK\right)$, Dijkstra의 경우 $\mathcal{O}\left(NK \log K\right)$만에 해결할 수 있습니다. 저는 그냥 Dijkstra로 해결했습니다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using uint = unsigned int;
using ull = unsigned long long;
using pii = pair<int, int>;
/* [t] [c] [s] */
pii seg[2000];
int last[1500], dist[1500][1500], dtemp[9000];
bitset<9000> vis;
void dijk(int s, const vector<vector<pii>> &graph) {
memset(dtemp, -1, sizeof dtemp);
vis.reset();
priority_queue<pii> pq;
dtemp[s] = 0;
pq.emplace(0, s);
while (pq.size()) {
int u = pq.top().second, d = -pq.top().first;
pq.pop();
if (dtemp[u] < d) continue;
if (vis[u]) continue;
vis[u] = true;
for (const auto &kv : graph[u]) {
int v = kv.first, c = kv.second;
if (dtemp[v] == -1 || dtemp[u] + c < dtemp[v]) {
dtemp[v] = dtemp[u] + c;
pq.emplace(-dtemp[v], v);
}
}
}
}
int main() {
cin.tie(nullptr);
cout.tie(nullptr);
ios_base::sync_with_stdio(false);
int tt;
cin >> tt;
for (int _ = 1; _ <= tt; _++) {
cout << "Case #" << _ << "\n";
memset(dist, -1, sizeof dist);
int n, k, q;
cin >> n >> k >> q;
vector<vector<pii>> graph(n);
for (int i = 0; i < n; i++) last[i] = i;
for (int i = 0; i < k; i++) {
cin >> seg[i].first >> seg[i].second;
seg[i].first--, seg[i].second--;
}
for (int i = 0; i < k; i++) {
const auto &l = seg[i];
int gn = graph.size();
graph[last[l.first]].emplace_back(gn, 1);
graph[last[l.second]].emplace_back(gn + 1, 1);
graph[last[l.first]].emplace_back(gn + 1, 0);
graph[last[l.second]].emplace_back(gn, 0);
last[l.first] = gn;
last[l.second] = gn + 1;
graph.emplace_back();
graph.emplace_back();
}
for (int i = 0; i < n; i++) {
graph[last[i]].emplace_back(graph.size(), 0);
last[i] = graph.size();
graph.emplace_back();
}
for (int i = 0; i < n; i++) {
dijk(i, graph);
for (int j = 0; j < n; j++) dist[i][j] = dtemp[last[j]];
}
int s = 0;
while (q--) {
int u, v;
cin >> u >> v;
u--, v--;
s += dist[u][v];
}
cout << s << endl;
}
return 0;
}
1차 4번 – 범위 안의 숫자
0에서 9까지의 숫자 $n \leq 50\ 000$개로 이루어진 문자열 $t$가 주어집니다. 길이가 $k \leq \min\left\{9,n\right\}$인 부분 문자열들을 수라고 생각하고, 모두 수직선 위에 둡니다.
이 때, 여기서 최대 한 글자까지를 1로 바꿔서, 어떤 정수 $a$에 대해 길이가 $m \leq 10^9$인 구간 $\left[a,a+m\right]$ 안에 속한 수의 개수의 최댓값이 최대가 되게 하고 싶습니다. 이 때의 최댓값을 구해야 합니다.
일단 $k$가 커봐야 $9$고, $n$도 그렇게 크지 않아서, 문자 하나를 1로 바꿀 수 있다는 것을 배제하고 생각하면 이 문제는 스위핑으로 해결할 수 있습니다. 부분 문자열의 값을 $x_i$라고 하면, 선분 $\left[x_i,x_i+m\right]$들을 수직선 위에 깔아 두고 가장 많이 겹쳤을 때의 선분의 갯수를 구하면 됩니다.
이제 문자 하나를 1로 바꿀 수 있는 경우를 생각해봅시다. ‘문자 하나를 1로 바꾸는 것’이라는 행위에서 관찰 가능한 특별한 성질은 딱히 없다고 느꼈습니다. 다만, 문자 하나를 1로 바꾸면 다시 만들어줘야 하는 선분의 개수는 $9$개에 불과하다는 사실에 집중했습니다.
만약 다이나믹하게 선분을 제거하고 추가할 수 있는 스위핑이 있다면, 모든 위치의 숫자를 하나하나 1로 바꾸고 되돌리는 행위를 한다고 해도 추가/제거는 $\mathcal{O}\left(kn\right)$번만 일어나므로 시간 안에 해결할 수 있을 것 같습니다.
다행히도 그런 스위핑은 존재하는데요, 최댓값을 구하는 연산과 구간에 덧셈을 하는 연산(lazy propagation 등)을 수행 가능한 세그먼트 트리로 가능합니다.
다만 인덱스가 꽤 크기 때문에 다이나믹 세그먼트 트리를 구현하거나, 가능한 값들을 전부 좌표 압축한 후 처리하는 방법을 사용해야 합니다. 저는 후자로 구현했습니다. 총 시간 복잡도는 $\mathcal{O}\left(kn \log kn\right)$입니다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using uint = unsigned int;
using ull = unsigned long long;
using pii = pair<int, int>;
/* [t] [c] [s] */
ll tree[1048576 * 2], lazy[1048576 * 2];
int c;
void _propagate(int x, int s, int e) {
if (!lazy[x]) return;
tree[x] += lazy[x];
if (s != e) {
lazy[x * 2] += lazy[x];
lazy[x * 2 + 1] += lazy[x];
}
lazy[x] = 0;
}
ll _maximum(int x, int s, int e, int l, int r) {
_propagate(x, s, e);
if (l > e || r < s) return 0;
if (l <= s && e <= r) return tree[x];
int m = (s + e) / 2;
return max(_maximum(x * 2, s, m, l, r),
_maximum(x * 2 + 1, m + 1, e, l, r));
}
void _update(int x, int s, int e, int l, int r, ll dv) {
_propagate(x, s, e);
if (l > e || r < s) return;
if (l <= s && e <= r) {
tree[x] += dv;
if (s != e) {
lazy[x * 2] += dv;
lazy[x * 2 + 1] += dv;
}
return;
}
int m = (s + e) / 2;
_update(x * 2, s, m, l, r, dv);
_update(x * 2 + 1, m + 1, e, l, r, dv);
tree[x] = max(tree[x * 2], tree[x * 2 + 1]);
}
ll maximum(int l, int r) {
return _maximum(1, 0, c - 1, l, r);
}
void update(int l, int r, ll dv) {
_update(1, 0, c - 1, l, r, dv);
}
ll zip(ll x, const vector<ll> &a) {
return lower_bound(a.begin(), a.end(), x) - a.begin();
}
ll v[50000], v1[50000][10];
int main() {
cin.tie(nullptr);
cout.tie(nullptr);
ios_base::sync_with_stdio(false);
int tt;
cin >> tt;
for (int _ = 1; _ <= tt; _++) {
cout << "Case #" << _ << "\n";
ll n, k, m;
cin >> n >> k >> m;
string t;
cin >> t;
// init values
vector<ll> ps;
ll curr = 0, mod = 1;
for (int i = 0; i < k; i++) mod *= 10;
for (int i = 0; i < k; i++) curr *= 10, curr += t[i] & 15, curr %= mod;
for (int i = k; i <= n; i++) {
v[i - k] = curr;
ps.emplace_back(curr);
ll l = curr, r = 0, p = 1;
for (int j = 0; j < k; j++) {
v1[i - k][j] = (l / 10 * 10 + 1) * p + r;
ps.emplace_back(v1[i - k][j]);
l /= 10, r += (curr / p) % 10 * p, p *= 10;
}
if (i == n) break;
curr *= 10, curr += t[i] & 15, curr %= mod;
}
int ts = ps.size();
for (int i = 0; i < ts; i++) ps.emplace_back(ps[i] + m);
sort(ps.begin(), ps.end());
ps.erase(unique(ps.begin(), ps.end()), ps.end());
memset(tree, 0, sizeof tree);
memset(lazy, 0, sizeof lazy);
c = ps.size();
// query
for (int i = 0; i <= n - k; i++) {
update(zip(v[i], ps), zip(v[i] + m, ps), 1);
}
ll mx = maximum(0, ps.size() - 1);
for (int i = 0; i < n; i++) { // replace i-th number to 1
// remove
for (int j = 0; j < k; j++) {
if (i - k + j < 0 || i - k + j > n - k) continue;
update(zip(v1[i - k + j][j], ps), zip(v1[i - k + j][j] + m, ps), -1);
}
if (i <= n - k) {
update(zip(v[i], ps), zip(v[i] + m, ps), -1);
}
// add
if (i - k >= 0) {
update(zip(v[i - k], ps), zip(v[i - k] + m, ps), 1);
}
for (int j = 0; j < k; j++) {
if (i - k + 1 + j < 0 || i - k + 1 + j > n - k) continue;
update(zip(v1[i - k + 1 + j][j], ps), zip(v1[i - k + 1 + j][j] + m, ps), 1);
}
// query
mx = max(mx, maximum(0, ps.size() - 1));
}
cout << mx << endl;
}
return 0;
}
aararaarar
🤐
와, 멋지십니다. 귀중한 코디 써주셔서 감사합니다.
저도 뜯어보면서 열심히 배우겠습니다~ ^^
트위터에서 주소 공유해 주신 거 보고 있습니다.
정말 많은 공부가 되고 있습니다. 저에게는 아직도 까마득~~~히 먼 길이네요.
소중한 자료 공유해주심에 다시 한 번 감사드립니다.
글 읽어 주셔서 감사합니다. 도움이 되셨다니 기쁩니다 😄