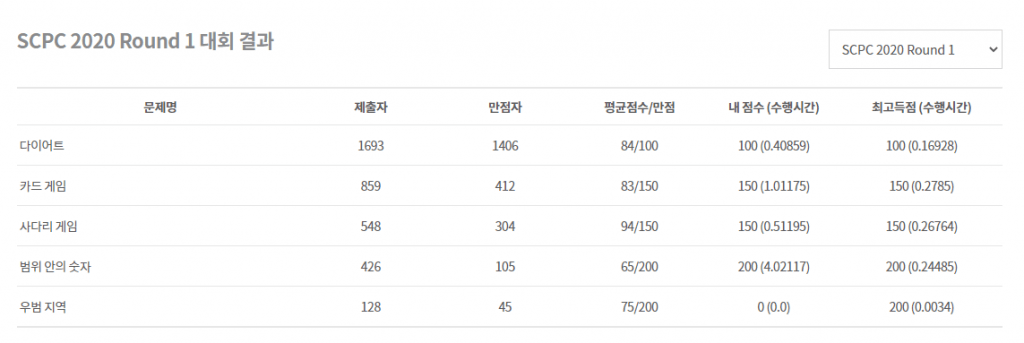
2차 예선에서 1, 2, 3, 5번을 풀어서 1,000점 만점에 750점을 받았습니다.
4번 문제보다 5번이 구현이 쉬워 보여서 5번을 먼저 해결했습니다. 이후 부분 점수를 보니 1번 + 2번 + 3번 + 4번 + 5번 47점 = 747점이었고, 이는 1번 + 2번 + 3번 + 5번 = 750점보다 적은 점수여서, 27위 안에 들었음을 확신하고 4번을 느긋하게 건들어 보다가 포기했습니다.
제 2차 1, 2, 3, 5번 풀이를 공유합니다. 4번 문제는 구현하지 않아서, 대략적인 아이디어만 갖고 있습니다.
2차 1번 – 실력 맞추기
각각 $N \leq 300\ 000$명의 멤버가 있는 A팀과 B팀이 있습니다. 멤버들은 각각의 실력 값을 갖고 있습니다. 이 때, A의 멤버를 최대 한 명까지 교체해서, A팀의 멤버 한 명과 B팀의 멤버 한 명씩을 매칭했을 때 전체 매칭의 실력 차의 합이 최소가 되게 하고 싶습니다.
두 가지 관찰을 할 수 있습니다.
- A팀에서 멤버 교체가 일어나지 않는 경우에는, A팀의 실력 값과 B팀의 실력 값을 각각 정렬해서 큰 순서대로 한 명씩 매칭해주는 것이 최적임은 자명합니다.
- 한 명을 교체하는 경우에는, 어떻게 교체하더라도 어떤 B팀 멤버가 있어서 그 멤버의 실력과 같도록 교체해 주는 것이 무조건 이득입니다. 그리고 이 경우 새롭게 매칭된 멤버들의 실력 차는 $0$입니다.
따라서 A팀에서 한 명을 교체한다기보다는, A팀과 B팀에서 한 명씩을 제외하고 나머지를 적절히 매칭하는 것을 생각할 수 있습니다. 이를 해결하기 위해 A팀과 B팀을 각각 정렬해 두고, 다음과 같은 다이나믹 프로그래밍을 생각할 수 있습니다.
- $dp\left(i,0\right)$: A팀과 B팀의 $\left[0, i\right]$의 멤버들을 각각 매칭했을 때의 실력 차의 합의 최솟값.
따라서 $dp\left(i,0\right) = dp\left(i-1,0\right) + \left|A_i-B_i\right|$입니다. - $dp\left(i,1\right)$: A팀 한 명을 제외하고, A팀의 $\left[0, i\right]$과 B팀의 $\left[0, i – 1\right]$의 멤버들을 각각 매칭했을 때의 실력 차의 합의 최솟값.
따라서 $dp\left(i,1\right) = \min\left\{ dp\left(i-1,0\right), dp\left(i-1,1\right) + \left|A_i-B_{i-1}\right| \right\} $입니다. - $dp\left(i,2\right)$: B팀 한 명을 제외하고, A팀의 $\left[0, i – 1\right]$과 B팀의 $\left[0, i\right]$의 멤버들을 각각 매칭했을 때의 실력 차의 합의 최솟값.
따라서 $dp\left(i,2\right) = \min\left\{ dp\left(i-1,0\right), dp\left(i-1,2\right) + \left|A_{i-1}-B_i\right| \right\} $입니다. - $dp\left(i,3\right)$: A팀과 B팀 중 각각 한 명씩을 제외하고, A팀과 B팀의 $\left[0, i\right]$의 멤버들을 각각 매칭했을 때의 실력 차의 합의 최솟값.
따라서 $dp\left(i,3\right) = \min\left\{ dp\left(i-1,3\right), dp\left(i-1,1\right), dp\left(i-1,2\right) \right\}$입니다.
이를 전부 계산하고 나면, 정답은 $dp\left(n,0\right)$과 $dp\left(n,3\right)$ 중 작은 쪽이 됩니다. 저는 1-based index를 사용해 구현했습니다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using uint = unsigned int;
using ull = unsigned long long;
using pii = pair<int, int>;
/* [t] [c] [s] */
int a[200001], b[200001];
ll dp[200001][4];
const ll inf = 1e18;
int main() {
cin.tie(nullptr);
cout.tie(nullptr);
ios_base::sync_with_stdio(false);
int t;
cin >> t;
for (int _ = 1; _ <= t; _++) {
cout << "Case #" << _ << endl;
int n;
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) cin >> b[i];
sort(a + 1, a + 1 + n);
sort(b + 1, b + 1 + n);
dp[1][0] = abs(a[1] - b[1]);
dp[1][1] = 0; // ignore a[i - 1]
dp[1][2] = 0; // ignore b[i - 1]
dp[1][3] = 0;
for (int i = 2; i <= n; i++) {
dp[i][0] = dp[i - 1][0] + abs(a[i] - b[i]);
dp[i][1] = min(dp[i - 1][0], dp[i - 1][1] + abs(a[i] - b[i - 1])); // ignore a[i - 1]
dp[i][2] = min(dp[i - 1][0], dp[i - 1][2] + abs(a[i - 1] - b[i])); // ignore b[i - 1]
dp[i][3] = min({dp[i][1], dp[i][2], dp[i - 1][3] + abs(a[i] - b[i])});
}
cout << min(dp[n][0], dp[n][3]) << endl;
}
return 0;
}
2차 2번 – 고구마
고구마 $N\leq 300\ 000$개가 일렬로 길게 연결되어 있습니다. 각 고구마의 가격은 $-10^{12} \leq A_i \leq 10^{12}$로 정해져 있습니다. 음수는 상품가치가 없어 발생하는 처리 비용입니다.
$M$만큼의 예산이 있어, 연결되어 있는 고구마 덩어리를 적절히 잘라 중간 덩어리를 사 가려고 합니다. 덩어리의 크기는 중요하지 않으나, 한 덩어리만 사갈 수 있습니다. 이 때 고구마를 적절히 잘라서, 예산 $M$을 넘지 않으면서 최대한 비싸게 사가고 싶습니다.
요약하면, 최대 구간합maximum subarray sum 문제인데, 합이 $M$보다 작거나 같으면서 최대한 큰 경우를 찾아야 합니다.
제한조건 때문에, 선형 시간에 최대 구간합 문제를 해결하는 Kadane’s 알고리즘은 사용할 수 없습니다. 다만 최대 구간을 구해야 한다는 점에서 구간합 배열prefix sum array을 이용해 접근해볼 수 있습니다.
구간합 배열 $P$를 만든 후, 현재 보고 있는 인덱스가 $i$라면, $P_i-P_j \leq M$이면서 $j < i$에 대해 $P_i-P_j$의 최댓값을 구해 주면 됩니다. 이는 std::set 자료 구조에 이전 인덱스까지의 구간합들을 전부 집어넣고, $\mathcal{O}\left(\log n\right)$이 걸리는 std::set::lower_bound을 사용해 쉽게 해결할 수 있습니다. 이유는 모르겠지만 저는 대회 당시에는 std::set::upper_bound를 사용해 구현했습니다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using uint = unsigned int;
using ull = unsigned long long;
using pii = pair<int, int>;
/* [t] [c] [s] */
int main() {
cin.tie(nullptr);
cout.tie(nullptr);
ios_base::sync_with_stdio(false);
int t;
cin >> t;
for (int _ = 1; _ <= t; _++) {
cout << "Case #" << _ << endl;
int n;
ll m;
cin >> n >> m;
set<ll> s;
s.emplace(0);
ll mx = 0, prf = 0;
for (int i = 0; i < n; i++) {
ll x;
cin >> x;
prf += x;
s.emplace(prf);
ll v = *s.upper_bound(prf - m - 1);
mx = max(mx, prf - v);
}
cout << mx << endl;
}
return 0;
}
2차 3번 – 아르바이트
안타깝게도 디스크립션이 정확히 기억나진 않는데요, $N \leq 200\ 000$ 크기의 배열 $A$가 주어지고, 특정 인덱스의 값을 바꾸는 연산을 $Q\leq 2\ 000$번 하려고 합니다. 이 때 각각의 연산마다 $A$의 길이 $K \leq \min\left\{200,N\right\}$의 모든 부분 배열의 구간합에 대해, 이들의 중앙값을 구해야 합니다. 단 가능한 부분 배열의 개수가 짝수 개라면, 중앙에 있는 두 값 중 더 큰 값을 구해야 합니다.
계속 변화하는 중앙값을 구해야 하는 문제로 BOJ 1572번이 있습니다. 이 문제의 경우 저는 크기가 같은 std::multiset을 두 개 만들어 두고, 한 쪽의 집합의 모든 원소가 다른 쪽의 집합의 모든 원소보다 작도록 유지해두는 방식으로 해결했습니다. 제 1572번 소스 코드는 여기에서 볼 수 있습니다.
원래 배열에 대한 생각은 접어 두고, 구간합들이 저장된 배열이 있다고 생각해 봅시다. 원래 배열에서 한 개의 원소가 바뀌면 구간합 배열에서는 최대 $K$개의 원소가 바뀝니다. $K \leq \min\left\{200,N\right\}$라는 조건 때문에, 전부 나이브하게 처리해 줘도 최대 $KQ \leq 400\ 000$번밖에 바뀌지 않으니 위와 같은 방법으로 열심히 짜면 맞을 수 있을 것이라 생각했고, 시간 초과를 받았습니다.
std::multiset의 삽입/삭제 연산의 복잡도는 $\mathcal{O}\left(\log n\right)$이지만, 상수가 크기 때문에 사용에 주의를 요합니다. 상수 커팅을 위해 다소 특이할 수 있는 세그먼트 트리를 생각해내 해결했습니다.
BOJ 1572번의 해법과 비슷하게, $mxt$와 $mnt$라는 세그먼트 트리를 각각 만들었습니다. $mxt$는 최댓값 세그먼트 트리, $mnt$는 최솟값 세그먼트 트리이며, 항상 $\max mxt \leq \min mnt$가 되도록 관리합니다. 그런데 이렇게 관리하려면, 만약 $\max mxt > \min mnt$일 때 $mxt$의 최댓값을 $mnt$의 최솟값과 바꿔 줘야 하고, 또한 특정 인덱스 $i$에 대해 값 업데이트도 가능해야 합니다.
이를 위해 트리의 노드에는 최대/최솟값과, 그 최대/최솟값이 들어 있는 배열에서의 인덱스를 저장하도록 했습니다. 또한, 랜덤 액세스를 쉽게 하기 위해, 두 세그먼트 트리의 크기는 $N-K+1$로 고정해 두고, 노드에 저장된 값이 $-1$인 경우 이 트리의 이 인덱스에 값이 존재하지 않음을 의미하도록 했습니다.
정해인지는 잘 모르겠습니다. 어떻게 잘 하면 느리게 갱신lazy propagation하는 테크닉을 섞어서 좀 더 빠르게 할 수도 있을 것 같기도 한데, 아래 코드도 만점을 받아서 더 이상 생각을 하지 않기로 했습니다.
들리는 말로는 크기 $NK$의 펜윅 트리로도 해결할 수 있다고 합니다. 하긴 펜윅이 빠르긴 빠르니까요.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using uint = unsigned int;
using ull = unsigned long long;
using pii = pair<int, int>;
/* [t] [c] [s] */
struct node {
int i, v;
node() : i(0), v(0) {}
node(int i, int v) : i(i), v(v) {}
bool operator<(const node &rhs) const {
return v < rhs.v;
}
};
node mnt[524288], mxt[524288];
int a[200001], val[200001], vals[200001];
ll prf[200001];
int tn, mxs, mns;
node minimum() { return mnt[1]; }
node maximum() { return mxt[1]; }
node argmin(const node &lhs, const node &rhs) {
if (lhs.v == -1) return rhs;
if (rhs.v == -1) return lhs;
return min(lhs, rhs);
}
node argmax(const node &lhs, const node &rhs) {
if (lhs.v == -1) return rhs;
if (rhs.v == -1) return lhs;
return max(lhs, rhs);
}
void setn(int i, int v, int x = 1, int s = 0, int e = tn - 1) {
if (s == e && s == i) {
mnt[x].v = v;
return;
}
if (i <= (s + e) / 2) {
setn(i, v, x * 2, s, (s + e) / 2);
} else {
setn(i, v, x * 2 + 1, (s + e) / 2 + 1, e);
}
mnt[x] = argmin(mnt[x * 2], mnt[x * 2 + 1]);
}
void setx(int i, int v, int x = 1, int s = 0, int e = tn - 1) {
if (s == e && s == i) {
mxt[x].v = v;
return;
}
if (i <= (s + e) / 2) {
setx(i, v, x * 2, s, (s + e) / 2);
} else {
setx(i, v, x * 2 + 1, (s + e) / 2 + 1, e);
}
mxt[x] = argmax(mxt[x * 2], mxt[x * 2 + 1]);
}
void update(int i, int dx, int x = 1, int s = 0, int e = tn - 1) {
if (s == e) {
if (mxt[x].v != -1) mxt[x].v += dx;
if (mnt[x].v != -1) mnt[x].v += dx;
return;
}
if (i <= (s + e) / 2) {
update(i, dx, x * 2, s, (s + e) / 2);
} else {
update(i, dx, x * 2 + 1, (s + e) / 2 + 1, e);
}
mxt[x] = argmax(mxt[x * 2], mxt[x * 2 + 1]);
mnt[x] = argmin(mnt[x * 2], mnt[x * 2 + 1]);
}
void init(int x = 1, int s = 0, int e = tn - 1) {
if (s == e) {
mnt[x].i = mxt[x].i = s;
if (s >= tn / 2) {
mxt[x].v = -1, mnt[x].v = vals[s];
mns++;
} else {
mnt[x].v = -1, mxt[x].v = vals[s];
mxs++;
}
return;
}
init(x * 2, s, (s + e) / 2);
init(x * 2 + 1, (s + e) / 2 + 1, e);
mxt[x] = argmax(mxt[x * 2], mxt[x * 2 + 1]);
mnt[x] = argmin(mnt[x * 2], mnt[x * 2 + 1]);
}
bool exchange() {
const auto mx = maximum(), mn = minimum();
if (mx.v <= mn.v) return false;
// set mntree
setn(mn.i, -1);
setn(mx.i, mx.v);
// set mxtree
setx(mx.i, -1);
setx(mn.i, mn.v);
return true;
}
int main() {
cin.tie(nullptr);
cout.tie(nullptr);
ios_base::sync_with_stdio(false);
int t;
cin >> t;
for (int _ = 1; _ <= t; _++) {
cout << "Case #" << _ << endl;
int n, k, q;
cin >> n >> k >> q;
tn = n - k + 1;
for (int i = 1; i <= n; i++) {
cin >> a[i];
prf[i] = prf[i - 1] + a[i];
}
for (int i = k; i <= n; i++) {
val[i - k + 1] = prf[i] - prf[i - k]; // [1, n - k + 1]
vals[i - k] = val[i - k + 1];
}
init();
while (exchange());
cout << minimum().v << ' ';
while (q--) {
int i, v;
cin >> i >> v;
int d = v - a[i];
for (int j = max(0, i - k); j < min(i, tn); j++) {
update(j, d);
}
while (exchange());
cout << minimum().v << ' ';
a[i] = v;
}
cout << endl;
}
2차 4번 – 안전운전
도로의 왼쪽, 오른쪽 경계와 운전 경로가 주어집니다. 도로 정보와 운전 경로는 선분들로 이루어져 있으며, 각각 $x$축 또는 $y$축과 평행합니다. 이 때, 운전 경로 중 특정한 가로선 하나 이하에 대해, 그 이후의 경로를 적절히 선대칭시켜서, 도로 안에 포함된 운전 경로의 세로선들의 길이의 합이 최대가 되게 하고 싶습니다. 단, 선대칭 이후의 도로 경로가 더 길어져서는 안 됩니다.
좌표 압축 후 위에서부터 아래로 내려오면서 스위핑 or 1차 4번과 비슷한 식의 세그먼트 트리를 이용하면 풀릴 거라고 생각했습니다. 하지만 1, 2, 3, 5번을 해결한 시점에서 이미 2차 예선 26위 이상임이 확정되었기 때문에 구현하다 포기했습니다.
2차 5번 – 삼각형의 거리
꼭지점 $N \leq 300$개의 단순다각형simple polygon이 있습니다. 오목할 수도 있습니다. 이 다각형의 꼭지점들을 이어 전부 삼각형으로 분할하고자 합니다.
어떤 삼각형에서 다른 삼각형과 맞닿은 변만을 통해 이동한다고 할 때, 삼각형 간의 거리를 정의할 수 있습니다. 예를 들어, 현재 삼각형과 맞닿아 있는 삼각형까지의 거리는 1이 됩니다. 처음 주어진 다각형을 잘 분할해서, 두 삼각형 사이의 최대 거리가 최소가 되도록 하고 싶습니다.
이 문제의 Small 셋의 경우, 다각형이 볼록다각형이므로 ICPC 2019 Korea Regional J번과 같은 문제입니다. 실제 대회에서 제가 First Solve로 해결했던 문제라 기억에 잘 남아 있던 것이 도움이 되었습니다.
다각형의 삼각 분할은 모든 노드의 $\deg \leq 3$인 트리로 나타낼 수 있습니다. 삼각 분할을 트리로 나타냈을 때, 이 트리의 지름을 최소화하는 문제가 됩니다.
주어진 도형을 어떤 대각선 하나로 자르면, 그 대각선 오른쪽에 만들어질 삼각형은 대각선 왼쪽에 만들 삼각형과 무조건 이어집니다. 이걸 바탕으로 2차원 다이나믹 프로그래밍을 생각해볼 수 있습니다. 현재 $i$번째 점 $P_i$부터 $j$번째 점 $P_j$까지만을 사용해 만든 도형이 있고, $\overline{P_iP_j}$는 어떤 다른 삼각형과 맞닿아있다고 생각해 봅시다. 한 쪽이 뚫려 있는 다각형이라고 생각하면 됩니다. 아래 그림의 핑크색 부분이 되겠네요.

이제 $dp \left(i,j\right)$를 핑크색 도형을 어떻게 잘 삼각분할했을 때 $\overline{P_iP_j}$에서 다른 삼각형까지의 최단 거리라고 정의합시다. 그러면 모든 $i<k<j$에 대해, 삼각형 $P_iP_jP_k$가 원래 다각형 안에 포함되는 경우 그 삼각형으로 분할한 뒤 재귀적으로 DP 문제를 해결할 수 있겠습니다.

따라서 $P_iP_jP_k$가 삼각형이 되는 모든 $i<k<j$들의 집합을 $K_{ij}$라 하면, 최단 거리는 $\overline{P_iP_k}$ 쪽에서 오거나 $\overline{P_kP_j}$ 쪽에서 오는 두 가지 경우가 있으므로, $dp\left(i,j\right)$는 다음과 같이 구할 수 있습니다.
\[dp\left(i,j\right)=\begin{cases} 0 & \textrm{if } i+1=j \\ \min_{k \in K_{ij}} \left\{ dp\left(i,k\right),dp\left(k,j\right) \right\}+1 & \textrm{otherwise} \end{cases}\]
하지만 이걸로는 트리의 지름을 구하기엔 역부족입니다. 왜냐하면, 이 다이나믹 프로그래밍의 경우 $\overline{P_iP_k}$에서 $\overline{P_iP_j}$ 쪽으로, $\overline{P_kP_j}$에서 $\overline{P_iP_j}$ 쪽으로 가는 건 고려하고 있지만, $\overline{P_iP_k}$에서 $P_iP_jP_k$를 거쳐 다시 $\overline{P_kP_j}$ 쪽으로 나가는 경로는 고려하지 못하고 있기 때문입니다.
점화식을 다시 정의해 봅시다. 어떤 값 $d$가 있어서, $dp_d \left(i,j\right)$를 다음과 같이 정의합니다.
\[dp_d\left(i,j\right)=\begin{cases} 0 & \textrm{if } i+1=j \\ \min_{k \in K_{ij}} \left\{ dp_d\left(i,k\right),dp_d\left(k,j\right) \right\}+1 & \textrm{if } dp_d\left(i,k\right)+dp_d\left(k,j\right) \leq d \\ \infty & \textrm{otherwise}\end{cases}\]
이제 이 점화식을 이용해 $dp_d\left(0,n-1\right)$를 구했고 그 값이 $\infty$가 아니라면, 트리의 지름이 $d$ 이하가 되도록 다각형을 삼각 분할할 수 있다는 뜻이 됩니다. 이제 이분 탐색으로 $d$의 최소값을 결정할 수 있습니다.
다이나믹 프로그래밍 한 번에 $\mathcal{O}\left(n^3\right)$이고, $0 \leq d \leq n-3$이므로 총 $\mathcal{O}\left(n^3 \log n\right)$만에 문제를 해결할 수 있습니다. 어떤 대각선이 오목다각형 안에 있는지 아닌지 판정하는 방법은 여러 가지가 있으나 문제의 포커스는 이게 아닌 것 같으므로 스킵하도록 합시다.
대회가 끝나고 안 사실인데 이 문제를 해결하는 논문이 있었다고 합니다.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using uint = unsigned int;
using ull = unsigned long long;
using pii = pair<int, int>;
/* [t] [c] [s] */
struct point {
int x, y;
point() : x(0), y(0) {}
point(int x, int y) : x(x), y(y) {}
point operator*(const int &rhs) const {
return {x * rhs, y * rhs};
}
point operator+(const point &rhs) const {
return {x + rhs.x, y + rhs.y};
}
point operator-(const point &rhs) const {
return *this + (rhs * -1);
}
};
int ccw(const point &a, const point &b, const point &c) {
point bb = b - a, cc = c - a;
ll t = (ll) bb.x * cc.y - (ll) cc.x * bb.y;
return t ? (t > 0 ? 1 : -1) : 0;
}
bool intersects(const point &la, const point &lb, const point &ma, const point &mb) {
if (ccw(la, lb, ma) * ccw(la, lb, mb) != -1) return false;
if (ccw(ma, mb, la) * ccw(ma, mb, lb) != -1) return false;
return true;
}
point A[300];
const int inf = 1e8;
int dp[300][300], dg[300][300];
bool diag(int i, int j, int n) {
if (i > j) swap(i, j);
if (dg[i][j] != -1) return dg[i][j];
if (i == j || i + 1 == j) return dg[i][j] = false;
if (i == 0 && j == n - 1) return dg[i][j] = false;
for (int v = 0, u = n - 1; v < n; u = v++) {
if (intersects(A[i], A[j], A[u], A[v])) return dg[i][j] = dg[j][i] = false;
}
point V1 = A[(i + 1) % n] - A[i], V2 = A[(i + n - 1) % n] - A[i], V3 = A[j] - A[i];
ll a = (ll) V1.x * V2.y - (ll) V1.y * V2.x;
ll b = (ll) V1.x * V3.y - (ll) V1.y * V3.x;
ll c = (ll) V3.x * V2.y - (ll) V3.y * V2.x;
bool in = (a >= 0 && b >= 0 && c >= 0) || (a < 0 && !(b < 0 && c < 0));
if (!in) return dg[i][j] = dg[j][i] = false;
return dg[i][j] = dg[j][i] = true;
}
int f(int i, int j, int d, int n) {
if (i + 1 == j) return dp[i][j] = 0;
if (!(i == 0 && j == n - 1) && !diag(i, j, n)) return dp[i][j] = inf;
if (dp[i][j] != -1) return dp[i][j];
dp[i][j] = inf;
for (int k = i + 1; k < j; k++) {
if (!(i + 1 == k || diag(i, k, n))) continue;
if (!(k + 1 == j || diag(k, j, n))) continue;
if (f(i, k, d, n) + f(k, j, d, n) > d) continue;
dp[i][j] = min(dp[i][j], max(f(i, k, d, n), f(k, j, d, n)) + 1);
}
return dp[i][j];
}
bool sat(int d, int n) {
memset(dp, -1, sizeof dp);
return f(0, n - 1, d, n) != inf;
}
int g(int x) {
if (x == 3) return 0;
if (x == 4) return 1;
if (x == 5) return 2;
return g((x + 1) / 2) + 2;
}
int main() {
cin.tie(nullptr);
cout.tie(nullptr);
ios_base::sync_with_stdio(false);
int t;
cin >> t;
for (int _ = 1; _ <= t; _++) {
cout << "Case #" << _ << endl;
int n;
cin >> n;
memset(dg, -1, sizeof dg);
for (int i = 0; i < n; i++) {
cin >> A[i].x >> A[i].y;
}
if (n == 3) {
cout << 0 << endl;
continue;
}
int l = g(n), h = n - 3;
while (l < h) {
int m = (l + h) / 2;
if (sat(m, n)) {
h = m;
} else {
l = m + 1;
}
}
cout << l << endl;
}
return 0;
}
회사 프로젝트에서 KaTeX를 한 번 사용해 본 이후로 제 블로그의 모든 수식을 KaTeX로 바꾸고 있습니다. 렌더 속도가 훨씬 빨라졌고, 모바일에서 수식 자동 줄바꿈이 잘 됩니다. 개인적으로는 여러 면에서 MathJax보다 좋은 라이브러리라고 생각합니다.